ГОСУДАРСТВЕННЫЙ КОМИТЕТ СОВЕТА МИНИСТРОВ СССР ПО ДЕЛАМ СТРОИТЕЛЬСТВА
ТЕХНИЧЕСКИЕ УСЛОВИЯ
ОПРЕДЕЛЕНИЯ ВОЛНОВЫХ
ВОЗДЕЙСТВИЙ НА МОРСКИЕ И РЕЧНЫЕ СООРУЖЕНИЯ И БЕРЕГА
СН 92-60
Утверждены
Государственным комитетом Совета Министров по делам строительства 21 апреля
1960 г.
ГОСУДАРСТВЕННОЕ ИЗДАТЕЛЬСТВО ЛИТЕРАТУРЫ ПО СТРОИТЕЛЬСТВУ, АРХИТЕКТУРЕ И СТРОИТЕЛЬНЫМ МАТЕРИАЛАМ
Москва - 1960
Настоящие «Технические условия определения волновых воздействий на морские и речные сооружения и берега» составлены междуведомственной Комиссией по волновым воздействиям ка гидротехнические сооружения при Совете по проблемам водного хозяйства АН СССР в составе представителей Совета по проблемам водного хозяйства АН СССР, Московского инженерно-строительного института имени В. В. Куйбышева, Главного инженерного управления Военно-Морского Флота, Центрального научно-исследовательского института морского флота Министерства морского флота, Центрального научно-исследовательского института экономики и эксплуатации водного транспорта Министерства речного флота РСФСР, Центрального научно-исследовательского института транспортного строительства Министерства транспортного строительства СССР, Государственного океанографического института и Государственного гидрологического института Главного управления гидрометеослужбы при Совете Министров СССР, Института гидрологии и гидротехники АН УССР, Лаборатории гидрогеологических проблем АН СССР, ВОДГЕО АСиА СССР, Гидропроекта МСЭС, Гипроречтранса РСФСР и других научно-исследовательских, проектных и учебных институтов.
Содержание
Основные буквенные обозначения и размерности
γ - объемный вес воды в т/м3;
hгл - высота волны на глубокой воде в м;
h -то же, мелкой воде в м;
λгл - длина волны на глубокой воде в м;
λ - то же, мелкой воде в м;
τгл - период волны на глубокой воде в сек.;
τ - то же, мелкой воде в сек.;
сгл - скорость распространения волны на глубокой воде в м/сек;
с - то же, мелкой воде в м/сек;
v -скорость движения частиц воды в точке в м/сек;
![]() - крутизна волны;
- крутизна волны;
Н - глубина в м
Нкр - критическая глубина в м;
Нб - глубина над берменными массивами в м;
hН - высота наката волны в м
а - угол заложения откоса в град.;
т - котангенс угла заложения откоса;
h0 - возвышение средней волновой линии в м;
W10 - скорость ветра, измеренная на высоте 10 м над уровнем водоема, в м/сек;
D - длина разгона в км;
р - давление волны местное в т/м2;
Р - суммарное давление на опору в т;
W - взвешивающее избыточное давление волны в т/noг. м;
R - суммарное боковое избыточное давление волны в т/noг. м;
d -диаметр конструктивного элемента в м;
g - ускорение силы тяжести в м/секг
е - основание натуральных логарифмов.
Примечание. Буквенные обозначения средних значений величин приводятся с чертой сверху соответствующего обозначения (например, h, X и т.д.). В отдельных случаях буквой с чертой сверху обозначены также безразмерные величины, что оговаривается в соответствующих местах в тексте (например, х).
I. ОБЩИЕ УКАЗАНИЯ. ОПРЕДЕЛЕНИЯ
1. Настоящими Техническими условиями следует руководствоваться при определении воздействия ветровых волн на гидротехнические и другие сооружения, возводимые на морях, озерах, водохранилищах и реках, судовых волн на крепление откосов каналов, а также воздействия ветровых волн на берега водохранилищ.
2. В технических условиях приведены указания по определению расчетных параметров волн и волновых воздействий на различные конструкции сооружений и рекомендации по расчету переформирования берегов водохранилищ.
Примечания. 1. Рекомендации по расчету изменения параметров ветровых волн при проникновении в частично защищенные от волнения акватории приведены в приложении III.
2. Рекомендации по расчету береговых переформирований приведены в приложении IV.
3. Волновые воздействия, определенные по настоящим Техническим условиям, при проектировании сооружений I класса и, при надлежащем обосновании, также II класса, рекомендуется уточнять на основе лабораторных исследований и по возможности на основе длительных (не менее 2 лет) натурных наблюдений.
Классификация волн
3. Ветровые волны классифицируются следующим образом:
Ветровые волны - волны, которые возникают на поверхности воды под действием ветра. Они делятся на вынужденные, свободные и смешанные.
Вынужденные волны - волны, находящиеся под воздействием ветра.
Свободные волны (зыбь) - волны, распространяющиеся после прекращения ветра или вышедшие из зоны его воздействия.
Вынужденные волны в начальной стадии их развития и волны зыби относятся к двухмерным (плоским) волнам.
При увеличении скорости ветра двухмерные волны превращаются в трехмерные (пространственные) волны, но при дальнейшем увеличении скоростей ветра и продолжительности его действия снова могут переходить в двухмерные.
Смешанные волны - волны, представляющие собой результат сложения вынужденных и свободных волн; они относятся к трехмерным волнам.
При взаимодействии волн с сооружениями происходит частичное или полное отражение их от сооружения (отраженные волны).
Интерферированные волны - волны, образующиеся oт сложения частично отраженных волн с подходящими волнами.
Стоячие волны - волны, являющиеся частным случаем интерферированных воли. Они образуются при подходе нескольких волн постоянной высоты и длины к сооружению с вертикальной или крутонаклонной стенкой, если гребни волн параллельны стенке. Высота их превышает высоту исходной волны в 2 раза при сохранении длины исходных волн.
При определенных глубинах на некотором расстоянии перед сооружением волны переходят в прибойные волны - волны, постоянно или периодически несущие на себе бурун. При резком изменении глубины у самого сооружения или в его пределах волны разбиваются о сооружение (разбитые волны).
Судовые или корабельные волны - особый вид волн, возникающих на поверхности воды при движении судов. Они бывают: расходящиеся, возникающие в носовой и отчасти в кормовой части судна и распространяющиеся под острым углом к направлению движения судна, и поперечные, возникающие в основном за кормой судна и направленные нормально к оси движения судна.
Терминология
4. В технических условиях принята следующая терминология (рис. 1):

Рис. 1. Профиль волны зыби
высота волны h - вертикальное расстояние между вершиной и подошвой волны;
длина волны λ - горизонтальное расстояние между двумя смежными вершинами или подошвами волны;
гребень волны - часть волны, расположенная выше статического уровня;
вершина волны - самая высокая точка
гребня волны;
впадина (ложбина) волны - часть волны между двумя гребнями, расположенная ниже статического уровня;
подошва волны - самая низкая точка впадины волны;
крутизна волны ![]() - отношение высоты волны к ее длине;
- отношение высоты волны к ее длине;
средняя волновая линия - горизонтальная линия, делящая высоту волны пополам;
фронт волны - линия вершины гребня волны в плане;
период волны τ - время, по истечении которого повторяется весь процесс колебания; для прогрессивных волн - промежуток времени, в течение которого гребень волны перемещается по горизонтальному направлению на расстояние длины волны;
скорость распространения волны с - скорость перемещения гребня волны по горизонтальному направлению без учета скорости течения;
разгон ветровых волн D - протяженность водной поверхности, охваченной ветром, вызывающим образование и развитие волн.
5. Характеристика водоемов и зон действия ветровых зон в прибрежной полосе глубокого водоема:
глубокие водоемы - водоемы с глубинами ![]() практически не
оказывающими влияние на волнение;
практически не
оказывающими влияние на волнение;
мелкие водоемы - водоемы с глубинами воды ![]()
Прибрежная полоса волнового поля глубокого водоема делится на четыре зоны:
первая зона - глубоководная с глубинами ![]() дно в этой зоне
практически не влияет на форму и размеры волн;
дно в этой зоне
практически не влияет на форму и размеры волн;
вторая зона - мелководная с глубинами ![]() > Н >Нкр; в этой зоне трехмерные
волны под влиянием дна преобразуются в двухмерные;
> Н >Нкр; в этой зоне трехмерные
волны под влиянием дна преобразуются в двухмерные;
третья зона - зона прибойных волн с глубинами Н ≤ Нкр.
В области критических глубин этой зоны (Н ≈ Нкр) • при которых крутизна волны достигает предельной величины, происходит опрокидывание гребня волны с образованием буруна.
Прибойная волна, продолжая двигаться к берегу, периодически забурунивается. При этом наряду с колебательным появляется поступательное движение частиц воды в сторону берега.
Нкр для второй и третьей зон определяется по п. 25;
четвертая зона - приурезовая, в которой происходит окончательное разрушение волны и образование наката прибойного потока на берег (откос).
Нкр, при которой происходит окончательное разрушение волн, определяется: на естественном берегу - по п. 25, на откосах - по п. 48;
мелководье - часть водоема с глубинами ![]() Я (в том числе вторая, третья и четвертая зоны прибрежной
полосы глубокого водоема).
Я (в том числе вторая, третья и четвертая зоны прибрежной
полосы глубокого водоема).
Виды волновых воздействий на сооружения и берега
6. При проектировании морских и речных сооружений следует учитывать следующие виды волновых воздействий:
а) воздействия на сооружения типа вертикальной стенки неразбитой стоячей, разбитой и прибойной волны;
б) воздействия на сооружения откосного типа;
в) воздействия на отдельно стоящие опоры и сквозные конструкций неразбитой, разбитой и прибойной волны и прибойного потока;
г) воздействия на берегоукрепительные сооружения волновых потоков разбитой волны;
д) воздействия на основания и отдельные элементы сооружений (массивы, откосы, каменную наброску, настилы и т. п.) при подходе и накате волны, всплесках, переливе и т. п.;
е) воздействия судовых волн на откосы и крепления каналов;
ж) переформирование берегов.
Примечания. 1. При проектировании сооружений, подверженных воздействию волн, производятся следующие поверки их устойчивости и прочности:
а) поверка обшей устойчивости сооружений типа вертикальной стенки и отдельных их частей, поверка оснований на сдвиг и напряжений в основаниях сооружений;
б) поверка устойчивости отдельных элементов откосных сооружений - камней, массивов, плит, подстилающего слоя, а также прочности плит и других элементов креплений земляных сооружений;
в) поверка на высоту наката волн на откос или подъема волны у сооружений, не допускающих перелива через них волы;
г) поверка на прочность отдельных элементов конструкций сквозных сооружений;
д) поверка на размыв донными скоростями дна перед сооружением;
е) другие поверки устойчивости и прочности сооружений и их частей в зависимости от типа и конструкций сооружений, а также местных условий.
2. Для сооружении, эксплуатация которых осуществляется в условиях волнения, производится поверка влияния волнения на режим работы этих сооружений (водосливные и водозаборные устройства и т.п.).
II. ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ ВЕТРОВЫХ ВОЛН
Общие указания
7. Волнообразующими факторами являются скорость ветра, продолжительность его действия и разгон волн.
На развитие и распространение волн оказывают влияние глубины, рельеф и шероховатость дна в направлении разгона.
Скорости ветра и продолжительности его действия для разных направлений определяются на основе статистической обработки данных наблюдений за ветром в безледные периоды на гидрометеорологических станциях. В результате этой обработки получают характеристики повторяемости и продолжительности ветров по градациям скоростей и направлений.
Примечание. Предпочтительными являются данные наблюдений гидрометеорологических станций, расположенных на островах и низких берегах.
8. Расчетная максимальная скорость ветра W10 в м/сек, вводимая в расчет при определении элементов ветровых волн, а также при определении ветрового нагона, для нормальных условий эксплуатации принимается с расчетной вероятностью превышения:
а) для сооружений I и 11 классов - 2% (1 раз в 50 лет);
б) для сооружений III и IV классов - 4% (1 раз в 25 лет);
в) для сооружений V класса - 10% (1 раз в 10 лет).
При форсировании уровней в момент пропуска наивысшего расчетного расхода расчетная максимальная скорость ветра для сооружений I - IV классов принимается равной среднемноголетней максимальной скорости ветра, наблюденной в сроки форсированных уровней за период we менее 10 лет.
При наличии коротких рядов наблюдений расчетные скорости ветра указанных выше обеспеченностей определяют на основе графической экстраполяции наблюденной части кривой распределения скорости ветра.
Для речных сооружений в указанных случаях допускается также определять расчетные скорости ветра по «Нормам и техническим условиям для расчета максимальных расходов воды при проектировании гидротехнических сооружений на реках» (СН 2-57).
Примечания. 1. Обеспеченность скорости ветра рассчитывается из условия, что в одну навигацию (год) возможен один случай максимальной скорости.
2. Расчетная максимальная скорость ветра для сооружений I и II классов при нормальных условиях эксплуатации должна приниматься не меньше той наблюденной максимальной скорости определенной продолжительности, при которой устанавливается наибольшее значение элементов волн. Наибольшие возможные размеры элементов волн в данном районе определяются при наиболее неблагоприятном сочетании значений скорости ветра, его продолжительности и разгона, устанавливаемых по результатам расчета.
3. При определении волновых воздействий на сооружения учитываются колебания уровней воды, вызываемые нагоном, сгоном, приливами, отливами, попусками, форсированием расходов и т. п.
9 Измеренные над водоемами скорости ветра должны приводиться к одной и той же высоте (10 м) над уровнем водоема.
Приведение производится по формуле
|
|
(1) |
где WH - скорость ветра, измеренная на высоте Н;
kw - коэффициент приведения, принимаемый в зависимости от высоты Н по табл. 1.
Таблица 1
Значения коэффициента kw
|
Н в м |
2 |
6,5 |
8 |
10 |
12 |
17 |
28 |
|
kw |
1,25 |
1,05 |
1,03 |
1 |
0,98 |
0,94 |
0,89 |
10. При определении расчетных скоростей ветра над водоемами по данным наблюдений материковых станций, в эти данные вводятся поправочные коэффициенты на основании имеющихся материалов или результатов специальных исследований.
Примечание. При пользовании данными наблюдений скоростей ветра на флюгерных станциях должен производиться пересчет этих данных на показания анемометрических станций.
11. Продолжительность действия ветра может не учитываться при расчете элементов ветровых волн мелких водоемов, а при расчете элементов волн глубоких водоемов - для разгонов до 100 км при скоростях менее 25 м/сек.
12. Разгон волны определяется по направлениям восьми основных румбов и по направлению наибольшей протяженности.
При наличии по линии разгона местного резкого сужения водоема разгон D принимается равным
|
D ≈ 5В, |
(2) |
где В - минимальная ширина водоема по разгону, но не более 5λ1%
При этом величина разгона D должна приниматься не меньше длины разгона до сужения.
При наличии мелководных участков в районе сужений влияние глубин (рефракция волн) может учитываться согласно приложению III, пп. 9 и 10.
13. Для определения разгона в условиях морей и больших водохранилищ рекомендуется производство анализа ветровых условий над всем водоемом и в случае необходимости - построение карт ветровых полей.
Скорость ветра по разгону допускается принимать постоянной при ее колебаниях в пределах ± 10%, а также при значениях скоростей, меньших 25 - 30 м/сек, для разгонов менее 100 км.
Определение разгонов по пути распространения волн с учетом рефракции в случаях возможного изменения прямолинейного распространения волн на криволинейное под действием препятствий, а также мелководий может производиться согласно приложению III, п. 9 и 10.
Направление распространения волн считается совпадающим с направлением ветра в пределах ± 22,5°.
Ориентировочные предельные значения разгонов для некоторых водоемов на территории СССР приведены в таблице приложения 1.
Примечание. Для приближенных расчетов рекомендуются следующие предельные сочетания разгонов и расчетных максимальных скоростей ветра:
|
|
Разгон D в км |
Скорость W10 в м/сек |
|
Для океанов |
1500 |
25 |
|
» морей |
600 |
30 |
|
» глубоких водохранилищ |
100 |
30 |
14. При оценке влияния глубины водоема в пределах разгона волн учитываются колебания уровней (п. 8, прим. 3).
Определение нагона Δh может производиться по зависимости
![]()
где величина k,
зависящая от относительной
глубины ![]() принимается по данным
специальных исследований. Ориентировочные значения k находятся в пределах 6 • 10-3 - 12
• 1-10-3; а - угол между осью водоема и направлением ветра.
принимается по данным
специальных исследований. Ориентировочные значения k находятся в пределах 6 • 10-3 - 12
• 1-10-3; а - угол между осью водоема и направлением ветра.
15. Для различных интервалов и повторяемостей скоростей ветра, его различных направлений, разгонов и профилей дна определяются элементы волн по каждому направлению (по пп. 20 - 26). Повторяемость этих элементов волн
принимается совпадающей с повторяемостью ветра данного румба, данной скорости и продолжительности.
16. Кроме учета обеспеченности элементов волн на тот или другой промежуток времени (например, год), учитывается также их обеспеченность в данной системе воли, характеризуемая количеством волн рассчитанных размеров при непрерывном и последовательном прохождении 100 волн через заданную точку.
17. Распределение элементов двухмерных волн в данной их системе, которая состоит не менее чем из 100 волн, последовательно проходящих через одну и ту же точку «а поверхности водоема, выражается вероятностными характеристиками (функциями их обеспеченности).
Функции распределения элементов двухмерных волн на глубоких водоемах и в глубоководных зонах по их обеспеченности приведены в табл. 2.
Таблица 2
Функции (безразмерные) обеспеченности параметров двухмерных волн на глубоких водоемах и в глубоководных зонах
|
Обеспеченность элемента в % |
|
|
|
|
1 |
2,52 |
1,65 |
6,5 |
|
2 |
2,28 |
1,57 |
4,8 |
|
5 |
1,91 |
1,47 |
2,75 |
|
10 |
1,69 |
1,37 |
1,9 |
|
20 |
1,38 |
1,23 |
1,3 |
|
30 |
1,21 |
1,15 |
0,96 |
|
40 |
1,05 |
1,07 |
0,77 |
|
50 |
0,93 |
1 |
0,62 |
|
60 |
0,81 |
0,93 |
0,51 |
|
70 |
0,69 |
0,85 |
0,4 |
|
80 |
0,51 |
0,76 |
0,3 |
|
90 |
0,37 |
0,66 |
0,2 |
|
95 |
0,23 |
0,58 |
0,15 |
|
99 |
0,1 |
0,44 |
0,04 |
Указания о распределении элементов двухмерных волн в условиях мелких водоемов и мелководных зон приведены в п. 26.
18. Определение высоты трехмерных волн различной обеспеченности на глубоких водоемах и в глубоководных зонах производится путем пересчета значения высоты двухмерных волн по табл. 3.
Таблица 3
Статистическая связь между значениями высот трехмерных и двухмерных волн в точке
|
Обеспеченность высоты двухмерной волны в точке в % |
Коэффициент перехода к высоте трехмерной волны |
Обеспеченность высоты двухмерной волны в точке в % |
Коэффициент перехода к высоте трехмерной волны |
|
1 |
1,1 |
50 |
1,3 |
|
5 |
1,14 |
60 |
1,34 |
|
10 |
1,18 |
70 |
1,42 |
|
20 |
1,2 |
80 |
1,51 |
|
30 |
1,23 |
90 |
1,73 |
|
40 |
1,27 |
95 |
1,98 |
На трехмерное волнение рассчитываются сквозные сооружения и сооружения, стоящие на относительно глубоководных участках.
Средняя высота двухмерных волн h и трехмерных волн hт в точке связаны между собой отношением
|
|
(3) |
Примечание. Допускается при надлежащем обосновании пользоваться и другими функциями обеспеченности элементов волн.
19. Расчетная обеспеченность высоты волны в данной системе волн для характеристики волнового режима принимается равной 1%.
По возможности учитывается также обеспеченность периода и длины (крутизны) волны, рассчитываемых по соответствующим формулам для высоты волны 1 % обеспеченности.
Расчетная обеспеченность высоты волны в данной системе при расчете гидротехнических сооружений принимается в зависимости от типа сооружений по соответствующим указаниям норм и технических условий на проектирование этих сооружений, но не 1менее 1%. При этом для расчета сооружений, для которых волновые нагрузки являются определяющими при расчете устойчивости и прочности, расчетная обеспеченность высоты волны принимается равной 1%.
При расчете сооружений на действие волн требуется также обоснованный выбор крутизны волны, соответствующей расчетной высоте волны.
Примечания. 1. Для условий глубоких
водоемов и глубоководных зон допускается принимать для ориентировочных расчетов
следующие значения крутизны волны ![]()
океаны
…………………………………………………………………………….…..![]()
моря
………………………………………………………………………..…..………![]()
большие водохранилища
………………………………………………….…………![]()
Уточнение приведенных соотношений производится на основании соответствующих расчетов (см. пп. 20 - 22, 25).
2. В преобладающем большинстве случаев наибольшим высотам штормовых волн соответствуют и наибольшие их крутизны.
Для расчета сооружений принимается наибольшая возможная на данном расстоянии от наветренного берега высота волны.
Определение параметров волн в глубоководной (первой) зоне
20. Если длина волны, полученная по расчету в данной точке, не превышает глубины водоема более чем в 2 раза, параметры волн для условий неустановившегося волнения определяют по известной скорости ветра, его продолжительности и разгону по п. 21, а для случая наиболее опасного установившегося волнения (при длительном воздействии ветра) - по п. 22.
21. Параметры волн определяются по графикам рис. 2 - 4.
По графику (рис. 2) определяется тип волнения (установившееся или развивающееся) на расстоянии D от наветренного берега. Безразмерные функции Т1 и ξ1, с помощью которых входят в этот график, вычисляются по зависимостям
|
|
(4) |
|
|
(5) |
где τ∞ = 0,52W10;
tw - время действия ветра в часах.
Волнение считается развивающимся, если точка с координатами T1 и ξ1 ложится ниже кривой а и установившимся, если выше этой кривой.

Рис. 2. График для определения типа волнения

Рис. 3. График для определения относительной высоты волны развивающегося волнения
Для развивающегося
волнения относительная высота волны ![]() определяется по рис.
3; h∞ принимается равным 0,02 W102
определяется по рис.
3; h∞ принимается равным 0,02 W102
Средняя длина волны ![]() определяется из
соотношения
определяется из
соотношения ![]() по рис 4.
по рис 4.

Рис. 4. График для определения крутизны волны
22.
Для наиболее опасного случая установившегося волнения высота волны hгл1% и средняя длина волны hгл безразмерном
виде) определяется по рис. 5 в зависимости от безразмерной величины ![]() где D - разгон в м.
где D - разгон в м.
Переход к значениям параметров волн любой другой обеспеченности производится согласно п. 17.
Периоды волн τгл определяются по рис. 6.
Скорость
распространения волн ![]()
При сложной ветровой обстановке и наличии установившейся и неустановившейся зон волнения параметры волн определяются согласно п. 21 и дополнительно для случая установившегося волнения - по рис. 7.

Рис. 5. График для определения параметров волн установившегося волнения

Рис. 6. График для определения периода волны по заданной высоте и длине волны

Рис. 7. График для определения относительной высоты волны установившегося волнения
Определение параметров волн в мелководной (второй) зоне
Рис. 8. Основные типы профилей дна
23. Определение параметров волн на водоемах с малыми глубинами (рис. 8, а, б) при волнообразовании производится следующим способом.
Высота волны h1% определяется по графикам (рис. 9 - 12), построенным для скоростей ветра 10, 20, 30 и

Рис. 9. График для определения высоты волны мелкого моря при W10 - I0 м/сек

Рис. 10. График для определения высоты волны мелкого моря при W10=20 м/сек

Рис. 11. График для определения высоты волны мелкого моря при W10=30 м/сек
40 м/сек (для других скоростей ветра высота волны определяется по интерполяции).
При изменении глубины по длине разгона профиль дна водоема в направлении разгона разбивается на участки с примерно одинаковыми глубинами или уклонами дна.
Переход к высоте волн иной обеспеченности производится по указаниям п. 26.
Среднюю крутизну волны определяют по графику рис. 13.

Рис. 12. График для определения высоты волны мелкого моря при W10=40 м/сек
Примечания 1. Значения параметров волн в области глубин ![]() корректируются в
соответствии с расчетами по пп. 21 и 22.
корректируются в
соответствии с расчетами по пп. 21 и 22.

Рис. 13. График для определения пологости волн мелкого моря
2. При Н ≤ Нкр расчет трансформации прибойных воля производится согласно п. 25.
3. В мелководных зонах со сложным рельефом дна при расчете параметоов волн в необходимых случаях учитывается явление рефракции (приложение III, пп. 9 и 10).
4. Метод, приведенный в п. 23, не применяется для расчета трансформации волн.
Расчет трансформации параметров волн глубокого водоема в мелководных зонах с постепенно убывающими глубинами
24. Определение параметров волн мелководной зоны с постепенно убывающей глубиной (рис. 8, в) при уклонах дна в пределах i=0,1 ÷ 0,001 производится по установленным значениям параметров волн глубоководной зоны в зависимости от глубины в данной точке. При уклонах i < 0,001 определение параметров волн производится по п. 23.
Расчет трансформации волн без учета рефракции производится методами, изложенными в пп. 25 и 26. Влияние рефракции на трансформацию учитывается отдельно (по приложению III, пп. 9 и 10).
25. Расчет трансформации волны на мелководных участках с начальными параметрами на глубокой воде hгл, λгл, τгл = τ с учетом влияния крутизны волны, а также определение глубины первого и последующих забуруниваний производятся последовательно по рис. 6, 14 - 19.
Значения ![]() (рис. 14 и 15)
определяются в зависимости от пологости волны
(рис. 14 и 15)
определяются в зависимости от пологости волны ![]() на глубокой
воде по рис. 6.
на глубокой
воде по рис. 6.
Глубина забурунивания волн зыби без ветра (граница между второй и третьей зонами) определяется по кривой 2 рис. 14 и 15 или по кривой 1 рис, 16. Критическая глубина воли с любым исходным значением hгл/τ2 может быть получена с помощью кривой 3 рис 14 и 15.
Предельные значения глубины забурунивания волн при сильном попутном ветре определяются по кривой 2 рис. 16.
Глубина забурунивания волн при сильном встречном ветре имеет значение, меньшее Нкр, определенной по кривой I рис. 16.
Высота волны на глубинах Н < Hкр определяется по рис. 14 и 15 с учетом уменьшения высоты волны при каждом забурунивании, определяемого отношением

Рис. 14. График для определения изменения высоты волны при трансформации

Рис. 15. График для
определения изменения высоты волны при трансформации - крупный масштаб для ![]()

Рис. 16. График для
определения критической глубины волн исходной крутизны ![]()

Рис. 17. График для определения изменение длины волны при трансформации

Рис. 18. График для определения возвышения гребня волны при трансформации
![]()
где h1 - высота волны на глубине, близкой к Hкр, до забурунивания;
h2 - высота волны на глубине, близкой к Hкр, после ее уменьшения при забурунивании. Значения k. определяемые по данным натурных наблюдений, находятся в пределах k < 0,85.
Уклону дна 0,05 соответствует значение k = 0,2, уклону 0,01 – k = 0,8.
Расчетное значение ![]() для волны после ее
забурунивания на глубине разрушения определяется по найденному h2/τ2 и
кривым 3 и 4 рис. 14 и 15 [см. ключ (2) и (3) к рис. 14].
для волны после ее
забурунивания на глубине разрушения определяется по найденному h2/τ2 и
кривым 3 и 4 рис. 14 и 15 [см. ключ (2) и (3) к рис. 14].
Высота прибойных волн, постоянно несущих на себе бурун, определяется по кривой 4 рис. 14 и 15 [см. ключ (1) и (4) к рис. 14].
Длина волн во второй
и третьей зонах определяется по рис. 17 и ![]() и найденным значениям
h/τ2.
и найденным значениям
h/τ2.
Возвышение гребня
волн зыби hгр над
статическим уровнем определяется в зависимости от высоты волны в данной точке
(полученной по рис. 14 и 15) и параметров ![]() и
и ![]() по рис. 18. Граница
разрушения волн зыби определяется кривой 1; при сильном попутном ветре
она может занимать предельное положение, соответствующее кривой 2.
по рис. 18. Граница
разрушения волн зыби определяется кривой 1; при сильном попутном ветре
она может занимать предельное положение, соответствующее кривой 2.
Для ветровых волн полученное
значение ![]() увеличивается на 10%.
увеличивается на 10%.
X Возвышение гребня волны после забурунивания определяется по новым расчетным значениям h, h/H, h/τ вплоть до последнего разрушения. Изменение возвышения гребня прибойной волны определяется по кривой 1 или 2 - рис. 18, в зависимости от ветровых условий и по полученным по рис. 14 и 15 значениям высот прибойных волн.
Определение
максимальной горизонтальной составляющей скорости частиц воды у гребня (vmax) производится по рис. 19 в зависимости от скорости распространения волны
![]()
Рис. 19. График для определения максимальной горизонтальной составляющей скорости движения частиц воды у гребня волны

Рис. 20. График для определения изменения спектра высот волн при трансформации
26. Расчет трансформации спектра волн глубокого водоема и распределения волн в спектре при выходе их на мелководье до четвертой зоны при уклонах дна 0,1 - 0,01 производится по рис; 20 - 22.
Определяются
значения средней высоты волн в спектре hгл, принимаемые постоянными до зоны окончательного разрушения, и среднего
периода волн ![]() для глубоководной
зоны.
для глубоководной
зоны.
По значению ![]() определяемому по рис. 20, находится высота волны заданной
обеспеченности.
определяемому по рис. 20, находится высота волны заданной
обеспеченности.
Изменение среднего
периода спектра волн ![]() в зависимости от
в зависимости от ![]() принимается по рис.
21.
принимается по рис.
21.
Для определения
длины волн любой обеспеченности λi% на заданной глубине H сначала находится по ![]() значение
значение ![]() на глубокой воде:
на глубокой воде: ![]() По значению
По значению ![]() определяют по рис. 21
величину
определяют по рис. 21
величину ![]() По
По ![]() находят
находят ![]() затем по
кривой 1 рис. 17 находят %, принимая
затем по
кривой 1 рис. 17 находят %, принимая ![]()
Длина волн заданной
обеспеченности h%
находится по отношению ![]() по рис. 22.
по рис. 22.
Глубина окончательного разрушения волн (граница между третьей и четвертой зонами) принимается равной 1,3 h.

Рис, 21. График для определения изменения среднего периода спектра волн при трансформации

Рис. 22. График для определения изменения спектра длин волн при трансформации
III. ОПРЕДЕЛЕНИЕ ВОЛНОВЫХ ВОЗДЕЙСТВИИ НА СООРУЖЕНИЯ ТИПА ВЕРТИКАЛЬНОЙ СТЕНКИ
А. Воздействие неразбитой стоячей волны
27. Расчет сооружения на давление неразбитой стоячей волны производится при глубине на берме Нс ≥ 2 h или глубине над поверхностью берменных массивов Нб > 1,5 h (рис. 23) для расчетного случая фронтального подхода волны к сооружению, если длина сооружения (L в м) вдоль фронта волны L ≥ λ.
Примечание. Кроме изложенного в подразделе «А» метода расчета, допускается пользоваться:
а) методом определения давления стоячих водч, приведенным в приложении II «а» в случаях, когда H ≥ 0,13λ;
б) для предварительных расчетов методом определения давления стоячих волн, основанном на линейной теории (метод Сенфлу в первом приближении), с введением для случая подхода гребня волны к стенке поправочных коэффициентов k определяемых по табл. 4.
Таблица 4
Значения коэффициента k
|
H/λ |
h/λ |
0,08 |
0,067 |
0,05 |
0,04 |
0,033 |
|
0,1 |
0,89 |
0,94 |
1,01 |
1,07 |
1,13 |
|
|
0,15 |
0,79 |
0,83 |
0,83 |
0,95 |
1 |
|
|
0,2 |
0.73 |
0,75 |
0,82 |
0,87 |
0,93 |
|
|
0,25 |
0,72 |
0,73 |
0,79 |
0,84 |
0,88 |
|
Вертикальная стенка
а) При подходе гребня волны к стенке (рис. 23).
28. Эпюра избыточного давления на стенку показана на рис. 23. Избыточное давление в точке zpz изб определяется по формуле
|
|
(6) |
где zpz изб - избыточное давление в точке z;
pz - полное давление с учетом гидростатического в точке z;
рГ - гидростатическое давление в точке z при статическом уровне.

Рис. 23. Эпюра волнового давления на вертикальную стенку (случай подхода гребня стоячей волны)
Величина рz определяется по формуле
|
|
(7) |
где t - время в долях периода τ;
|
|
(8) |
|
|
(9) |
|
|
(10) |
|
|
(11) |
|
|
(12) |
|
|
(13) |
|
|
(14) |
|
|
(15) |
Примечание. Значения п, т и Θ могут определяться также по рис. 1 - 6 приложения II «б»
Значение sin σ t можно определить в зависимости от а и β по рис. 24;
Возвышение гребня
волны ![]() над статическим
уровнем во всех случаях определяется по рис. 25.
над статическим
уровнем во всех случаях определяется по рис. 25.
Суммарное избыточное боковое давление, действующее со стороны подхода волны, определяется по формуле
|
|
(16) |
|
где |
(17) |
|
|
(18) |
29. Если линии α и β (рис. 24) не пересекаются, то максимум полного давления наступает в момент наивысшего положения гребня волны у стенки, что соответствует значению
![]()
В этом случае величина полного давления в точке определяется по формуле
|
|
(19) |
где
|
|
(20) |
Суммарное боковое избыточное давление Re вычисляется по формуле(Ш), в которой Re определяется по формуле
|
|
(21) |
Значение φ определяется по формуле (20).

Рис. 24

Рис. 25
30. Избыточное взвешивающее давление при подходе гребня волны к сооружению, возведенному на каменной на броске, определяется по формуле
|
|
(22) |
где рс.гр вычисляется по формуле (19) при z = Hc .
Примечание. При определении взвешивающего давления в настоящем и последующих пунктах надлежит учитывать следующие положения:
а) при покрытии бермы со стороны акватории порта берменными массивами расчетная ширина стенки В увеличивается на ширину покрытия массивами;
б) в формулу для определения взвешивающего давления может водиться на основе специальных исследований коэффициент полноты эпюры, определяемый в зависимости от толщины, типа постели и длины волны;
в) взвешивающее давление на отдельные курсы массивовой кладки определяется на основе специальных исследований.
31. При глубинах перед сооружением ![]() эпюра бокового
избыточного давления может быть построена по трем точкам ро.гр, рс.гр,
zгр (см. рис. 23):
эпюра бокового
избыточного давления может быть построена по трем точкам ро.гр, рс.гр,
zгр (см. рис. 23):
|
|
(23) |
|
|
(24) |
где zгр - возвышение волновой поверхности над статическим уровнем, вычисляется по рис. 25;
![]() - определяются по рис. 26 и 27 в зависимости
от а и β. Суммарное боковое избыточное давление определяется
по формуле
- определяются по рис. 26 и 27 в зависимости
от а и β. Суммарное боковое избыточное давление определяется
по формуле
|
|
(25) |
Примечание. Опрокидывающий момент от давления Re определяется по формуле
|
|
(26) |

Рис. 26
б) При подходе впадины волны к стенке (рис. 28)
32. Эпюра избыточного давления на стенку представлена на рис. 28.
Избыточное боковое давление в точке z pz изб определяется сто формуле
|
|
(27) |
|
|
(28) |
|
|
(29) |

Рис. 27

Рис. 28. Эпюра волнового давления на вертикальную стенку (случай подхода впадины стоячей волны)
Наинизшее положение впадины волны
|
|
(29') |
где ![]() определяется
по рис. 29.
определяется
по рис. 29.
Суммарное боковое избыточное давление R определяется по формуле
|
|
(30) |
где
|
|
(31) |
Избыточное взвешивающее давление Wt определяется по формуле
|
|
(32) |
где рс.вп - определяется по формуле (28) при z = Hc.

Рис. 29
Примечания. 1. Опрокидывающий момент для берменных массивов вокруг внутреннего ребра от давления при подходе впадины волны определяется по формуле
|
|
(33) |
где η - коэффициент, определяемый в зависимости от kH и h/λ по табл. 5.
Таблица 5
Значения коэффициента η
|
|
H/λ |
≥ 0,06 |
< 0,06 |
|
< 1,7 1,7 - 2 > 2 |
0,43 0,3 0,15 |
0,32 0,22 0,15 |
|
I - длина берменного массива в м;
![]()
![]()
п принимается равным:
для первого ряда массивов ………………… 1
» второго » » ……………………… 2
2. Удерживающий момент My определяется по формуле
|
|
(34) |
где Тб - высота берменного массива;
γб - объемный вес бетона (в воздухе).
33. При глубинах перед сооружением ![]() эпюра бокового избыточного
давления может быть построена по точкам pвп, pс. вп, zвп (см. рис. 28):
эпюра бокового избыточного
давления может быть построена по точкам pвп, pс. вп, zвп (см. рис. 28):
|
|
(35) |
|
|
(36) |
где zвп определяется по формуле (29);
рн.вп определяется в зависимости от а и β по рис. 30 и 31.
Точка нулевого давления находится «а статическом уровне.
Суммарное баковое избыточное давление Ri определяется по формуле
|
|
(37) |
Взвешивающее избыточное давление при подходе впадины волны к сооружению, возведенному на каменной наброске, определяется по формуле
|
|
(38) |
где рс.вп, вычисляется по формуле (36).
Примечание. Опрокидывающий момент от давления Ri определяется по формуле
|
|
(39) |
34. Бели при малых относительных глубинах
перед сооружением ![]() возможны расчетные
волны очень малой крутизны
возможны расчетные
волны очень малой крутизны ![]() для расчета
сооружении I и II классов в этих условиях требуется проведение
специальных исследований.
для расчета
сооружении I и II классов в этих условиях требуется проведение
специальных исследований.

Рис. 30
В указанных случаях для приближенных вычислений давления на статическом уровне р0 и у дна рн определяются по рис. 32, где zl = H + hгр
35. При наличии волнения со стороны водоема и со стороны акватории порта за расчетное суммарное избыточное давление «а стенку принимается
![]()
Если наибольшее Давление имеет место со стороны водоема, то Re определяется по параметрам волн со стороны водоема, a Ri - по параметрам волн со стороны акватории порта; при наибольшем давлении со стороны акватории порта Re определяется по параметрам волн со стороны акватории порта, a Ri -со стороны водоема.
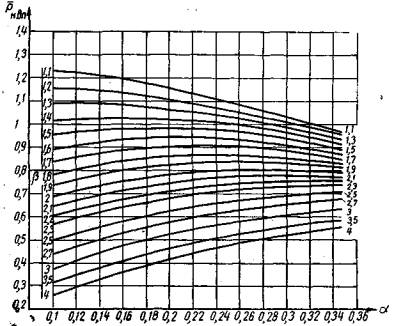
Рис. 31
Примечание. При определении расчетного давления следует учитывать характер волнения с внутренней стороны стенки и возможность образования стоячих волн
36. Максимальное возвышение гребня волны над статическим уровнем принимается равным
|
|
(40) |
максимальное понижение впадины волны у стенки от статического уровня принимается равным
|
hвп = h-h0, |
(41) |
где
|
|
(42) |

Рис. 32. График для определения волнового давления на вертикальную стенку при малых относительных глубинах
37. Максимальная донная скорость υmax на расстоянии ![]() перед
сооружением определяется по формуле
перед
сооружением определяется по формуле
|
|
(43) |
где n определяется по табл. 7.
Крутонаклонная стенка (90° > a > 45°)
38.
Расчет волнового давления на крутонаклонную стенку при 5h > H ≥ 2h и ![]() может производиться
следующим приближенным методом.
может производиться
следующим приближенным методом.
По вычисленным для вертикальной стенки давлениям в точках на статическом уровне и у дна строится эпюра вол нового давления (рис. 33) и определяется значение ординаты волнового давления p3h на глубине H = 3h по формуле
|
|
(44) |
где р0 и рн - давления на вертикальную стенку на статическом уровне и на уровне дна, определяемые по указаниям приложения II а.
Величина волнового давления на крутонаклонную стенку на указанной глубине H = 2>h в зависимости от величины а определяется по формуле
|
|
(45) |
Ниже глубины H = 3h величина давления p3ha принимается постоянной.
Давление на статическом уровне p′0 для любых значений а принимается равным
|
p′0 = p0 |
(46) |
и направлено нормально к стенке. Выше и ниже этого уровня изменение давления принимается по линейному закону.

Рис. 33. Расчетная схема волнового давления на крутонаклонную стенку
39. Высота подъема уровня воды zB у крутонаклонной стенки при максимуме волнового давления принимается равной высоте волны.
40. Взвешивающее волновое избыточное давление определяется по треугольной эпюре аналогично указаниям пп. 30 и 32.
Примечание. Для конечной стадии проектирования рекомендуется лабораторная проверка устойчивости сооружений, для расчета которых величины волнового давления определены изложенным выше способом.
41. Эпюра давления, построенная для стенки, которая поставлена на призму, уменьшается в нижней части на высоту этой призмы, а при наличии парапета на стенке и перелива воды через него срезается на уровне парапета.
42. Высота наката на крутонаклонную стенку определяется по формуле
|
|
(47) |
где h0 - принимается по формуле (42).
Б. Воздействие разбитой волны
43. Расчет сооружений на давление разбитой волны производится при глубине над поверхностью берменных массивов Hб < 1,5 h и глубине перед сооружением H > Hкр.
Эпюра избыточного давления при разбитой волне показана на рис. 34.
Избыточное боковое давление на статическом уровне определяется по формуле
|
|
(48) |
Избыточное давление на уровне верха берменных массивов на глубине Hб принимается равным
|
|
(49) |
Избыточное давление на уровне основания стенки на глубине Нс принимается равным
рс = 0,75 рб .

Рис. 34. Эпюра волнового бокового и взвешивающего давлений при разбитой волне
Высота подъема свободной поверхности у стенки в момент максимального давления принимается равной
|
|
(50) |
Взвешивающее избыточное давление принимается равным
|
|
(51) |
где В - ширина стенки в основании;
μ - коэффициент полноты эпюры, принимаемый равным:
при ![]() < 3 …………………………………………………… 0,7
< 3 …………………………………………………… 0,7
» ![]() от 3 до 5
………………………………………………. 0,8
от 3 до 5
………………………………………………. 0,8
» ![]() от 5 до 7
……………………………………………… 0,9
от 5 до 7
……………………………………………… 0,9
» ![]() ≥ 7………………………………………………………
1
≥ 7………………………………………………………
1
(здесь толщина постели Т = Н - Hс).
В. Воздействие прибойной волны
44. Расчет сооружения на действие прибойной волны производится при Н ≤ Hкр.

Рис. 35. Эпюра волнового бокового и взвешивающего давлений при прибойной волне
Параметры волн в этом случае определяются согласно п. 25.
Эпюра избыточного давления на вертикальную стенку представлена на рис. 35.
Избыточное боковое давление в точке ![]() над статическим
уровнем определяется по формуле
над статическим
уровнем определяется по формуле
|
|
(52) |
где υ' - орбитальная скорость, принимаемая равной
|
|
(53) |
давление у дна рH = ![]() нулевое давление
принимается в точке над статическим уровнем z1 = h′.
нулевое давление
принимается в точке над статическим уровнем z1 = h′.
Суммарное боковое избыточное давление определяется по формуле
|
|
(54) |
избыточное взвешивающее давление принимается по треугольной эпюре равным
|
|
(55) |
где ц - коэффициент полноты эпюры, принимаемый равным 0,7.
Высота максимального всплеска волны у стенки над статическим уровнем определяется по формуле
|
|
(56) |
Момент максимального всплеска принимается не совпадающим с максимальным давлением.
45. При наличии в основании сооружения каменной призмы, возвышающейся над дном, эпюра давления строится для значений H перед сооружением, но в расчетах принимается часть эпюры, расположенная выше уровня подошвы стенки (совпадающей с верхом призмы), аналогично рис. 23.
Примечание. Кроме методов расчета, изложенных в пп. 43 - 44, может применяться при надлежащем обосновании соответствующих коэффициентов так называемый динамический метод расчета, которым учитываются динамические импульсы и инерционные силы.
IV. ОПРЕДЕЛЕНИЕ ВОЛНОВЫХ ВОЗДЕЙСТВИИ НА СООРУЖЕНИЯ ОТКОСНОГО ТИПА
46. Приводимые в настоящем разделе указания по определению волновых воздействий относятся к фронтальному воздействию волн на откосы с крутизной 1,5 ≤ m < 5 (при степени отражения r ≤ 0,5).
Примечания. 1. Определение волновых воздействий на более пологие откосы производится на основе специальных исследований.
2. В данном разделе расчетные параметры волн h и λ относятся к глубине H перед откосом сооружения.
47. Глубина H1 вслед за которой происходит значительное увеличение скоростей на откосе, определяется по формуле
|
|
(57) |
Зона от глубины H1 до высоты наката волны на откос считается областью интенсивного волнового воздействия.
48. Критическая глубина Hкр, на которой происходит разрушение волны, определяется по формуле
|
|
(58) |
49. Величина отражения волны от откоса r, увеличивающаяся с уменьшением крутизны волны и увеличением крутизны откоса, определяется по формуле
|
|
(59) |
где kш - коэффициент, учитывающий шероховатость и проницаемость откоса, принимается по табл. 6;
hотр - высота отраженной волны на глубокой воде, определяемая:
для откосов круче 1 : 3,7 по формуле
|
|
(60) |
для откосов положе 1 : 3,7 по формуле
|
|
(61) |
Таблица 6
|
Характеристика откоса (тип покрытия) |
kш |
|
Сплошное непроницаемое гладкое покрытие (асфальтобетон) |
1 |
|
Бетонное покрытие |
0,9 |
|
Мостовая (каменная кладка) |
0,75-0,8 |
|
Наброска из округлых камней (булыжник) |
0,6 - 0,65 |
|
Наброска из рваного камня |
0,55 |
|
» » массивов |
0,5 |
При глубине перед сооружением ![]() высота отраженной
волны перед откосом hoтp определяется, используя рекомендации п. 25 и
по известной высоте hотр. гл.
высота отраженной
волны перед откосом hoтp определяется, используя рекомендации п. 25 и
по известной высоте hотр. гл.
50. При воздействии волн на сооружение откосного типа могут иметь место следующие условия отражения волн от откоса:
а) отсутствие отражения - при r ≤ 0,1, когда происходит полное разрушение волн на откосе;
б) незначительное отражение - при 0,1 < r < 0,5, когда разрушение преобладает над отражением;
в) значительное отражение - при 0,5 ≤ r < 1, когда отражение преобладает над разрушением;
г) полное отражение волн - при r = 1.
51. Удар струи, сбрасываемой с гребня волны при ее разрушении на откосе, определяется для точки В откоса на глубине Hкр - уB
В зоне, близкой к точке В, наблюдается максимальная скорость и наибольшая интенсивность давления в момент удара.
Координаты точки В (рис. 36) определяются уравнениями
|
|
(62) |
|
|
(63) |
где y0 -ордината точки А, характеризующая положение струи в начальный момент сброса ее с гребня волны:
|
|
(64) |
hгр - возвышение точки над статическим уровнем:
|
|
(65) |
υA - горизонтальная проекция начальной скорости струи, сбрасываемой с гребня волны,
|
|
(66) |
где п - эмпирический коэффициент, вычисляемый по формуле
|
|
(67) |

Рис. 36. Разрушение волны зыби по наклонной стенке
52. Эпюра скоростей на откосе при ударе волны об откос представлена на рис. 37.
Максимальная скорость струи при ударе ее об откос, наблюдающаяся в точке В, определяется по формуле
|
|
(68) |
где хв - определяется по формуле (63);
υа - определяется по формуле (66);
η - коэффициент, учитывающий уменьшение скорости при растекании струи в скатывающемся потоке:
|
|
(69) |
Максимальная скорость струи на статическом уровне в момент наката определяется по формуле
|
|
(70) |
где кщ принимается по табл. 6,
Скорости струи выше статического уровня принимаются убывающими по линейному закону
|
|
(71) |
где l - расстояние вверх по откосу от статического уровня до искомой точки;
hH - высота наката волны, определяемая по формуле (73).

Рис. 37. Эпюра скоростей на откосе
Скорости струи по откосу ниже статического уровня, начиная от глубины z = H1 (рис. 37) до подошвы сооружения, определяются по формуле
|
|
(72) |
где п - коэффициент, принимаемый в зависимости от пологости волны по табл. 7.
Таблица 7
|
λ/h |
8 |
10 |
15 |
20 |
|
п |
0,6 |
0,7 |
0,75 |
0,8 |
На участке ниже точки В скорости принимаются убывающими по линейному закону.
При крутонаклонных стенках (m < 1,5) и пологих волнах, при которых возможно увеличение скорости, верхний предел скорости соответствует скорости стоячей волны (случай полного отражения).
53. Максимальная высота наката волны h H на откосы (без берм) отсчитывается от статического уровня и определяется по формуле
|
|
(73) |
где кш - коэффициент, принимаемый по табл. 6.
Расчетная обеспеченность параметров волн устанавливается в зависимости от типа и класса сооружений (п. 19).
При определении ![]() учитываются указания
пп. 20
- 22,
25.
учитываются указания
пп. 20
- 22,
25.
Примечание. При косом подходе волн высота наката hн должна определяться с учетом угла подхода волн.
54. Максимальное местное давление рB шах на откос от удара струи в точке В в момент обрушении волны определяется по формуле
|
|
(74) |
где φ - угол между касательной к направлению струи в точке В и нормалью к откосу, равный
|
φ = 90° - (a + β); |
(75) |
β - абсолютное значение угла между касательной к направлению струи в точке В и горизонталью, вычисляемое из уравнения
|
|
(76) |
55. Эпюра волнового давления на откос (рис. 38) строится по точкам с давлением рв шах и с давлениями, вычисленными для расстояний от точки В вверх до точек ξ1 и ξ2 и вниз до точек ξ3 и ξ4, имеющими соответственно значения 0,4 рВ mах и 0,1 рВ тях.

Рис. 38. Эпюра волнового давления на откос в момент удара волны
Эти расстояния по откосу равны
ξ1 = 0,0255; ξ3 = 0,0535;
ξ2 = 0,0655; ξ4 = 0,1355,
где
|
|
(77) |
56. Суммарное максимальное давление на откос р в момент удара струи волны равно
|
p = pB тaх + pc, |
(78) |
где рс - статическое давление скатывающегося потока.
Эпюра статического давления скатывающегося с откоса потока представлена на рис. 39.
В момент непосредственно перед ударом ординаты эпюры равны:
в точке 0 (начало координат аналогично рис. 36) ….. Hотк;
в точке В ….. а;
на урезе при статическом уровне ….. 0,6 а;
где
|
Hотк = (0,1m + 0,2)h; |
(79) |
|
а = 0,055 mh. |
(80) |
57. Вес Q отдельных камней и массивов в набросных сооружениях с откосами 1:1 - 1:3, устойчивых против размывающего действия волн в зонте их обрушения (состояние предельного равновесия), определяется по формуле

Рис. 39. Эпюра статического давления скатывающегося с откоса потока воды
|
|
(81) |
где γм - объемный вес отдельного камня или массива;
μ - коэффициент, учитывающий форму камня, может приниматься равным 0,017 для массивов и 0,025 для каменной наброски.
V. ОПРЕДЕЛЕНИЕ ВОЛНОВЫХ ВОЗДЕЙСТВИИ НА ОТДЕЛЬНО СТОЯЩИЕ ОПОРЫ (СВАИ) И СКВОЗНЫЕ КОНСТРУКЦИИ
А. Опоры (сваи) и элементы сквозных конструкций с
диаметром сечения 
58.
Высота расчетной волны определяется для обеспеченности 1 % в зависимости от ![]() по рис. 20.
по рис. 20.
Расчетное значение возвышения гребня волны hгр относительно статического уровня определяется по рис. 40 с увеличением полученного результата на 0,5 м.
Профиль расчетной волны принимается по рис. 41.
Длина расчетной (наиболее опасной) волны принимается равной 10 hi% .
Волновая нагрузка, действующая на конструктивный элемент, принимается распределенной по его продольной оси.

Рис. 40. График для определения расчетного возвышения гребня волны

Рис. 41. Расчетные профили волны
Горизонтальная рх и вертикальная рz составляющие волнового давления в т/пог. м в какой-либо точке оси элемента находятся в общем случае как сумма горизонтальных и соответственно вертикальных составляющих скоростного и инерционного волновых давлений:
|
pх = px cк + pх ин; |
(82) |
|
pz = pz cк + pz ин. |
(83) |
а) Определение
волновых воздействий в зоне ![]()
59. При диаметре вертикальной опоры ![]() горизонтальная
скоростная составляющая волнового давления определяется по формуле
горизонтальная
скоростная составляющая волнового давления определяется по формуле
|
|
(84) |
где сх - коэффициент
лобового сопротивления, определяемый по рис. 42, в зависимости от числа ![]() в первом приближении сх может
приниматься равным:
в первом приближении сх может
приниматься равным:
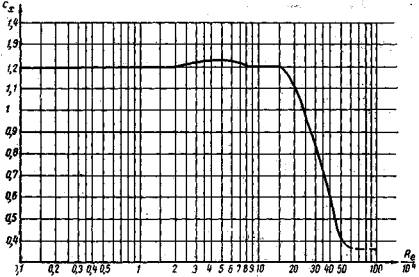
Рис. 42. График для определения коэффициента лобового сопротивления
при Re ≥ 6 · 105 0,36;
» Re < 6 · 105 .....1,2;
vx - горизонтальная составляющая скорости движения частиц воды в рассматриваемой точке, принимаемая по формуле
|
υx = υop6 + и, |
(85) |
где υx орб - горизонтальная составляющая орбитальной скорости, вычисляемая по формуле
|
|
(86) |
и - скорость поступательного движения:
|
|
(87) |
z0 - расстояние рассматриваемой точки от статического уровня вниз;
х - расстояние от опоры до гребня волны;
v - кинематический коэффициент вязкости.
Для построения эпюры скоростного давления рх ск вычисляются значения vх для ряда точек по высоте опоры, уточняются в случае необходимости значения Re в этих точках и определяются значения сх и рx ск.
При диаметре вертикальной опоры ![]() дополнительно
суммируется горизонтальная инерционная составляющая давления рх ин
дополнительно
суммируется горизонтальная инерционная составляющая давления рх ин
|
|
(88) |
где сн - коэффициент присоединенной массы воды, принимаемый для круглых опор равным 1,7;
jx - горизонтальная составляющая ускорения движения частиц воды в м/сек2, определяется по формуле
|
|
(89) |
px ин определяется по точкам эпюры скоростей υx и орбитальных ускорений jx для различных фаз прохождения волны (х = 0; х = 0; х = 0,125λ; х = 0,25λ; х = 0,5λ и т.д.) и по выбранным фазам алгебраически суммируется с рx ск для получения эпюры распределения рх по высоте опоры.
Расчетное значение рх принимается для фазы, соответствующей максимальному значению суммы рХ ск и рХ ин.
б) Определение
волновых воздействий в зоне ![]() от 0,25 до
0,8.
от 0,25 до
0,8.
60. При диаметре вертикальной опоры d < 0,5 м наибольшее общее горизонтальное Давление определяется по формуле
|
px max,i = 0,2γh2id, |
(90) |
где hi - расчетная высота волны.

Рис. 43. Изменение общего волнового давления на
вертикальный цилиндрический элемент в зависимости от безразмерной координаты ![]()
Изменение наибольшего общего горизонтального давления вдоль волнового луча учитывается в соответствии с рис. 43.
Ординаты эпюры волнового давления и плечо равнодействующей волнового давления относительно отметки дна определяются соответственно по формулам
|
z1 = бz |
(91) |
где
|
|
(92) |
z - длина «смоченной» вертикальной части опоры;
ax ск - коэффициент, определяемый в функции безразмерных Координат ![]() и
и ![]() :
:
при ![]() - по рис. 44;
- по рис. 44;
при ![]() - по рис. 45;
- по рис. 45;
при ![]() - по интерполяции;
- по интерполяции;
δ - коэффициент, определяемый в зависимости от безразмерной координаты ![]() . При
. При ![]() (рис. 44) его
значения находятся в пределах 0,57 – 0,65; при
(рис. 44) его
значения находятся в пределах 0,57 – 0,65; при ![]() δ = 0,85.
δ = 0,85.
В тех случаях, когда
параметр Рейнольдса, определяемый по формуле ![]() меньше 6 · 105,
скоростная составляющая давления умножается на 2,78 сх, где сх
- коэффициент лобового сопротивления, определяемый по рис. 42.
меньше 6 · 105,
скоростная составляющая давления умножается на 2,78 сх, где сх
- коэффициент лобового сопротивления, определяемый по рис. 42.
61. При диаметре вертикальной опоры d > 0,5 м, помимо скоростной составляющей волнового давления, следует учитывать дополнительно инерционное давление px ин пропорциональное (d2 - 0,52), которое определяется по формуле
|
|
(93) |
где
|
|
(94) |
|
При |
(95) |
|
при |
(96) |

Рис. 44

Рис. 45
β1 - коэффициент, определяемый по рис. 46 в функции координаты х, алгебраический знак β1 ставится перед радикалом.

Рис 46
62. Вертикальная составляющая волнового давления на горизонтальные круглоцилиндрические элементы сквозных конструкций рz, действующего в точке на оси элемента с безразмерными координатами х и z, определяется по формуле
|
Рz = Рz ск + Рz ин |
(97) |
где
|
рz ск = 0,009 аz ск β1 γhd; |
(98) |
|
рz ин = 0,16аz ин β2 γd2; |
(99) |
|
|
(100) |
|
|
(101) |
β1 и β2 - коэффициенты, определяемые по рис. 46.
63. Волновое давление в какой-либо точке на элементы конструкций, непараллельные координатным осям х и z, находится как сумма скоростного и инерционного давлений.
Скоростное давление определяется как геометрическая сумма горизонтальной и вертикальной составляющих:
|
|
(102) |
|
|
(10З) |
где рх ск и pz ск - горизонтальная и вертикальная составляющие давления;
φz и φх - углы, образуемые осью элемента с осями координат.
Составляющие рх и pz скоростного давления нормальны к оси элемента и действуют в плоскостях; содержащих ось элемента и соответствующую координатную ось.
Инерционное давление выражается как сумма горизонтального инерционного давления на плоскость yoz и вертикального инерционного давления на плоскость хоу. Составляющие инерционного давления определяются корректировкой значений рх ин и рz ин путем приведения к действительной длине элемента (делением на косинус угла между осью элемента и его проекцией на соответствующую плоскость).
в) Определение
волновых воздействий в зоне ![]()
64. Суммарное давление р на элемент конструкции определяется по формуле
|
|
(104) |
где F - площадь проекции погруженной в воду части элемента конструкции на вертикальную плоскость, нормальную к направлению потока;
υx - расчетная величина горизонтальной составляющей волновой скорости, принимаемой постоянной по глубине и равной vmax; определяется по рис. 19;
сх - коэффициент лобового сопротивления, принимается для элементов круглого сечения равным 0,36.
г) Опоры и элементы конструкции, отличные от круглоцилиндрических
65. При определении скоростных составляющих волнового давления на опоры и элементы конструкций, отличающихся по форме от круглоцилиндрических, в соответствующие расчетные формулы вводятся поправочные коэффициенты к, выражающие отношение коэффициентов лобового сопротивления элемента рассматриваемой формы и круглого цилиндра:
для квадратного и таврового сечения k - 1,7
для прямоугольного
сечения при соотношении сторон ![]() (рис. 47), и для
плоской полосы, ориентированной вдоль потока, k = 1,4
(рис. 47), и для
плоской полосы, ориентированной вдоль потока, k = 1,4
Для инерционных составляющих волнового давления учитывается влияние формы элемента на величину коэффициента присоединенной массы см.
д) Определение волновых воздействий на сквозные конструкции
66. Общее волновое давление на сквозную конструкцию определяется как геометрическая сумма волновых давлений на все смоченные элементы, определенных при одном и том же положении профиля волны относительно сооружения.
При расстояниях между осями отдельных вертикальных элементов, превышающих четыре поперечных размера элемента, волновое давление определяется в предположении независимости действия волны на отдельные элементы. При меньших расстояниях между осями элементов в рассчет вводится коэффициент k1, значения которого в зависимости от отношения расстояния между осями смежных опор l к диаметру опор d принимаются по табл. 8.
Таблица 8
Значения коэффициента k1
|
|
Значение l/d |
||
|
2 |
3 |
4 |
|
|
Ряд опор, параллельных фронту волны |
1,5 |
1,25 |
1 |
|
То же, перпендикулярных фронту волны |
0,7 |
0,8 |
1 |

Рис. 47. Вертикальные обтекаемые преграды
а - эпюра при Н < 0,3λ; б - поперечные сечения; в - эпюра при H >0,5λ
Б. Опоры (сваи.) и элементы сквозных конструкций с
диаметром 
67. Приводимые ниже
расчетные формулы для определения волновых воздействий на опоры и элементы
сквозных конструкции с диаметром сечения ![]() (эллиптические и
прямоугольные сечения при а и
(эллиптические и
прямоугольные сечения при а и ![]() ) применимы при следующих дополнительных ограничениях:
) применимы при следующих дополнительных ограничениях:
а) для вертикальных преград (рис. 47) при
![]()
б) для горизонтальных преград (рис. 48) при
![]()
где а - размер преграды в направлении луча волны;
b - размер преграды по нормали к лучу волны;
λ - длина волны в ближайшей к преграде зоне.
Примечание. Предельное значение давления на опору большого диаметра не должно превышать соответствующего давления на вертикальную стенку.
68. Суммарное волновое давление Р в момент времени t при угловой скорости а определяется по формуле
|
|
(105) |
где Pин. max и Рск. max - наибольшие значения соответственно инерционной и скоростной составляющих волнового давления, определяемые по формулам и графикам, приведенным в п. 69, в зависимости от сечения преграды и заданных параметров волн. Максимальное суммарное волновое давление Рmax принимается равным
|
|
(106) |
при
![]()
и
|
|
(107) |
при
![]()
Частные значения тригонометрических функций, соответствующих суммарному максимальному значению вол нового давления в некоторый момент времени t1 находятся по формулам
|
|
(108) |
|
|
(109) |
Для случая, когда суммарное максимальное давление определяется только инерционной составляющей (формула (106)],
sin σt1 = 1.
69. Наибольшие значения инерционной и скоростной составляющих суммарного волнового давления на вертикальную преграду полной высоты с поперечным сечением в виде круга, эллипса, квадрата или прямоугольника (рис. 47), рассчитываются по формулам
|
|
(110) |
|
|
(111) |
где εин и εск - коэффициенты обтекания, учитывающие увеличение волнового давления за счет перехода от эллиптического к прямоугольному поперечному сечению преграды; для преград в виде круглого и эллиптического цилиндров εин = 1 и εск =1; для призматических преград εин и εск определяются по рис. 49;
kν - поправочный коэффициент к величине скорости в зоне, ближайшей к
преграде, определяемый по рис. 50; при значении ![]() допускается принимать
kv=l;
допускается принимать
kv=l;

Рис. 48. Горизонтальные обтекаемые преграды

Рис. 49. Графики функций ![]()
аин и аск - коэффициенты,
учитывающие влияние отношения Н/λ на величину инерционной и
скоростной составляющих волнового давления, определяемые по рис. 51;
допускается принимать аин = 1 при ![]() - >0,3 и аск = 1 при
- >0,3 и аск = 1 при ![]()
βин и βск - коэффициенты формы, определяемые по рис. 49; для круглоцилиндрических преград βин = 1 и βск = 1.
70. Точка приложения силы Рmax находится по правилам сложения параллельных сил Рин и Рск.

Рис. 50. График для определения коэффициента ![]()
71. Относительные
вертикальные координаты линий действия инерционной и скоростной составляющих
суммарной силы ![]() и
и ![]() определяются как
функции от
определяются как
функции от ![]() по рис. 52.
по рис. 52.
72. Волновое давление на единицу длины горизонтальной свободно обтекаемой преграды (см. рис. 48) определяется геометрическим суммированием горизонтального и вертикального волновых давлений по формуле
|
|
(112) |
где р - равнодействующая, а рх и pz -горизонтальная и вертикальная проекции равнодействующей волнового давления в момент времени t.
Расчетные формулы для рх и pz в общем виде:
|
|
(113) |
|
|
(114) |
где px ин.max, px ск max, pz ин.max, pz ск max - соответственно горизонтальная и вертикальная проекции наибольших значений инерционной и скоростной составляющих волнового давления, рассчитываемые по формулам пп. 74 - 75.
73. Наибольшие значения горизонтальной px max вертикальной pz max проекций равнодействующей находятся по правилам, изложенным в п. 68.

74. Наибольшие значения инерционной и скоростной составляющих горизонтального волнового давления на единицу длины горизонтальной преграды, имеющей в поперечном сечении круг, эллипс, квадрат или прямоугольник, определяются по формулам

Рис. 52 График функций ![]()
|
|
(115) |
|
|
(116) |
где zц - расстояние от статического уровня до геометрического центра преграды;
εин, εск, kν, βин, βск - определяются согласно указаниям п. 69.
75. Наибольшие значения инерционной и скоростной составляющих вертикального волнового давления на единицу длины горизонтальной преграды, имеющей в поперечном сечении круг, эллипс, квадрат или прямоугольник, определяются по формулам
|
|
(117) |
|
|
(118) |
76. Построение эпюры распределения волнового давления по глубине для вертикальных преград (см. рис. 47) производится по вычисленным ординатам давления не менее чем для четырех точек по глубине, включая z = 0 и z = Н.
Возвышение волновой поверхности над статическим уровнем определяется по формуле
|
|
(119) |
Ордината эпюры волнового давления на глубине (z - ξ) определяется по формуле
|
|
(120) |
где рх ин. max и рх ск. max определяются по формулам (П5] и (116) при условии замены zц на z.
Примечание. При построении эпюры распределения волнового давления допускается принимать равными нулю скоростную составляющую ординат волнового давления на глубине, равной 0,3 λ, и инерционную - на глубине, равной 0,5 λ (см. рис. 47).
В. Учет влияния различных факторов
77. При определении
волнового давления на преграды с диаметром сечения ![]() учитывается влияние
обрастания преград (водорослями, ракушками, балянусом) путем увеличения
скоростной составляющей давления, действующего на часть опоры ниже
среднегодового уровня (учет увеличения шероховатости), при значительном
обрастании - на 40%, при небольшом обрастании - до 20%.; обрастание не
учитывается в случаях, когда предусматривается эффективная борьба с явлением
обрастания.
учитывается влияние
обрастания преград (водорослями, ракушками, балянусом) путем увеличения
скоростной составляющей давления, действующего на часть опоры ниже
среднегодового уровня (учет увеличения шероховатости), при значительном
обрастании - на 40%, при небольшом обрастании - до 20%.; обрастание не
учитывается в случаях, когда предусматривается эффективная борьба с явлением
обрастания.
Необходимо также учитывать в соответствующих расчетных формулах возможное увеличение расчетного сечения свай малых диаметров, за счет их обрастания в соответствии с местными условиями.
78. При расчете гибких сооружений, период собственных колебаний которых с учетом волнового воздействия больше или равен 1 сек., необходимо вводить соответствующую поправку на динамику сооружения.
VI. ОПРЕДЕЛЕНИЕ ВОЛНОВЫХ ВОЗДЕЙСТВИЙ НА БЕРЕГОУКРЕПИТЕЛЬНЫЕ СООРУЖЕНИЯ
79. Волновые воздействия на берегоукрепительные сооружения, расположенные в приурезовой (четвертой) зоне, для I и II классов сооружений определяются для условий обрушения волн прибоя наибольшей высоты ft, устанавливаемой по указаниям п. 25.
Для сооружений III - V классов разрешается пользоваться приближенными значениями расчетной высоты волн прибоя ft, определяемыми в зависимости от значения среднего уклона дна:
![]()
где S0 - ширина прибрежной полосы, в пределах которой исчисляется средний уклон;
H0 -глубина воды на расстоянии S0 от линии уреза.
Значения h могут приниматься равными:
при iср ≥ 0,04 ………………………………………………………………………….. 3 м
» icp = 0,03 …………………………………………………………………………….. 2,5 »
» icp ≤ 0,015 …………………………………………………………………………… 2 »
Расчетные значения h не должны превышать высоты волн, определяемой по расчету для глубоководной зоны водоема согласно указаниям по пп. 21, 22.
Примечания. 1. В условиях берегов с подводными валами высота h измеряется по первой, считая со стороны водоема, линии обрушения волн над подводным валом.
2. iср исчисляется для береговой полосы S0 = 100 м (рис. 53, а); когда на расстоянии 100 м от линии уреза расположен подводный вал,

Рис. 53. Схема участка приурезовой полосы
то icp исчисляется для полосы S0, увеличенной на расстояние до подошвы подводного вала с внешней его стороны (рис. 53, б).
3. В условиях берегов с уклонами icp<0,03, в тех случаях, когда внешняя грань сооружения располагается на расстоянии L > λ/2 от места разрушения волн с высотой, равной h, разрешается расчетную высоту волны принимать равной глубине Н0 на расстоянии λ/2 от внешней грани сооружения (рис. 54).

Рис. 54
4. Для берегов водохранилищ со сложным рельефом подводного склона, а также при наличии на нем уступов или банкетов расчетная высота волны h определяется по результатам соответствующих исследований.
80. Боковое давление прибойных волн р0 на вертикальные стенки берегоукрепительных сооружений на статическом уровне при фронтальном подходе волн определяется по формуле
|
p0 = 1,5γh. |
(121) |
Эпюра бокового давления по высоте представлена на рис. 55.

Рис. 55. Эпюра бокового давления на вертикальные стенки берегоукрепительных сооружений
Полное боковое давление определяется по формуле
|
R0 = l,5γ(0,75h + H)h. |
(122) |
За пределами приурезовой зоны волновые нагрузки определяются согласно указаниям раздела III.
81. При определении волновых давлений на поверхности сооружений, постоянно затопленных (при статическом уровне) или затопляемых при действии волнения, расчетная нагрузка снижается за счет обтекания сооружения волновым потоком в вертикальной плоскости на величину, зависящую от положения гребня сооружения относительно уровня водоема.
Давление на затопленную вертикальную стенку р0.з принимается равным
|
P0 = kHp0, |
(123) |
где kH - коэффициент уменьшения нагрузки, определяемый в зависимости от положения гребня сооружения относительно уровня водоема и расчетной высоты волны h по табл. 9.
Таблица 9
|
|
Положение гребня |
|||
|
на высоте 0,З h над уровнем воды |
на уровне водоема |
на глубине 0,3 h ниже уровня водоема |
на глубине 0,65 h и ниже |
|
Кh |
0,95 |
0,85 |
0,8 |
0,5 |
Давление на вертикальный уступ Рае берегоукрепительного волнолома со скошенными массивами (рис. 56) с учетом уменьшения давления за счет обтекания в вертикальной плоскости определяется по формуле
|
рАЕ = ар0, |
(124) |
где а - коэффициент, принимаемый при высоте уступа до 70 см равным 0,5. При этом давление Рае не должно быть меньшим давления на наклонную площадку волнолома (АВ), определяемого согласно указаниям п. 82. 82. Давление на элемент, наклоненный под углом 0 к вертикали, рβ (рис. 57), в случае расчета сооружений, расположенных на глубинах Н ≤ h с уклонами дна перед сооружениями не более 0,1 при фронтальном подходе волн, определяется по формуле
|
рβ = 0,5р0(1 + cos2 β). |
(125) |

При глубинах у внешней грани сооружения H > h и уклоне дна перед сооружением более 0,1 расчетная величина давления дополнительно определяется также по пп. 54 - 56 и за расчетное давление принимается большее из найденных по этим двум способам.

Рис. 58
83. Давление на криволинейную поверхность (рис. 58) определяется по формуле (125) путем построения эпюры давлении по отдельным точкам, для которых давления рх рассчитываются в зависимости от углов рх наклона касательных в этих точках к вертикали.
Давление с учетом косины подхода волн к сооружению
(рис. 59) определяется по формуле
|
pа = 0,5p0(1 + cos2a cos2 β), |
(126) |
где a - угол между направлением сооружения в плане и фронтом разрушающихся волн;
β - угол наклона плоскости внешней грани сооружения относительно вертикали. Косина подхода волн учитывается для поперечных конструкций (буны, траверсы волноломов и т. п.) в тех случаях, когда давление ра превышает давление, рассчитанное без учета косины подхода.

Рис. 59. Схема подхода волны к поперечным береговым сооружениям
Волновые воздействия на продольные береговые сооружения определяются без учета косины подхода волн. Наибольшее значение угла косины б (рис. 59) определяется на основании натурных наблюдений или по результатам теоретических и лабораторных исследований.
Примечание. Для берегов с уклоном дна iср большим 0,04, наибольшее значение угла 8 можно определить по рис 60.

Рис. 60. График для определения наибольшего угла подхода волн
85. В условиях
косого подхода волн учитывается неравномерность волновых воздействий по длине
поперечных сооружений умножением величины давления ра [формула
(126)] на коэффициент k1 определяемый в зависимости от отношения ![]() по табл. 10,
по табл. 10,
где S - длина элемента сооружения в м, равная длине массивов или, при конструкциях с пролетными перекрытиями - расстоянию между осями опор, воспринимающих горизонтальную нагрузку.
Таблица 10.
|
S/λ |
≤ 0,03 |
0,05 |
0,1 |
≥ 0,2 |
|
k1 |
1 |
0,75 |
0,65 |
0,6 |
Примечание. Для конструкции из набросок и стенок из свай принимается k1 = 1.
86. Взвешивающее волновое давление по подошве вооружения определяется по эпюре (см. рис. 56) с наибольшей ординатой бокового давления рда с внешней стороны сооружения. Ордината со стороны берега принимается равной
|
|
(127) |
87. Вертикальная составляющая волнового давления рв.з для всех затопленных волной частей сооружения определяется по формуле
|
|
(128) |
где k - коэффициент, принимаемый равным:
при расчете продольных сооружений ……0,75
» » поперечных …………………………..0,5.
88. Обратное волновое давление по задней (береговой) грани продольного сооружения (плоскость CD, см. рис. 56) в момент действия максимальных нагрузок с внешней стороны сооружения принимается равным нулю.
Обратное боковое давление на поперечные сооружения, устойчивость которых определяется в условиях наибольшей косины подхода волн к берегу в момент максимального давления на плоскость АБ (см. рис. 59) со стороны подхода волн, определяется по формуле
|
|
(129) |
где k2 - коэффициент уменьшения обратного бокового давления с теневой стороны за счет неравномерного его распределения вдоль поперечного сооружения и отставания по фазе (по сравнению с давлением со стороны подхода волн).
При проектировании сооружений I - II классов значения k2 определяются на основе соответствующих лабораторных опытов в волновых бассейнах или иными достаточно обоснованными способами.
Для сооружений III -V классов коэффициент k2 может быть определен по табл. 11 в зависимости от отношения S/X и от величины отставания волн по фазе btgδ (см. рис. 59) у теневой грани сооружения.
Здесь b -ширина сооружения в м;
S - принимается по п. 85;
δ - расчетный угол косины подхода волн.
Таблица 11
|
S/λ |
b tg б |
≤ 0,03 |
0,05 |
0,1 |
≥ 0,2 |
|
0 0,5 1,2 2,5 |
0,8 0,5 0,2 0 |
0,7 0,5 0,25 0 |
0,65 0,5 0,35 0 |
0,6 0,5 0,4 0 |
|
Примечание. Для конструкций из набросок принимается k2 = 0.
89. При расчетах продольных береговых сооружений следует учитывать обратное волновое давление, действующее при откате волны.

Рис. 61. Схема определения обратного волнового давления
Наибольшее обратное давление, направленное в сторону акватории водоема Wотк (рис. 61) для какой-либо точки х, измеряется гидростатически напором воды η в т/м2, равным
|
|
(130) |
где угр - расчетное возвышение гребня волны над статическим уровнем, принимаемое равным 0,75 h, но не более Hст;
ух - высотное положение точки х относительно статического уровня.
Знак (-) или (+) принимается соответственно для точек, расположенных выше или ниже статического уровня.
Понижение уровня в момент отката волны определяется по формуле
|
|
(131) |
где ап - коэффициент, принимаемый равным:
при отсутствии надводного пляжа перед стеной …..1
при ширине пляжа свыше 7 м ……………………….0
При учете обратного волнового давления волновое давление со стороны водоема считается отсутствующим.
Обратное волновое давление для стен, заложенных в водопроницаемых грунтах, учитывается на всю высоту сооружения от его верха до подошвы основания (рис. 61).
Обратное волновое давление на волнолом, действующее со стороны заволноломной акватории, измеряется гидростатическим напором воды, равным
|
|
(132) |
где z - высота волнового нагона воды за волноломом, определяемая по данным специальных исследований.
VII. ОПРЕДЕЛЕНИЕ ВОЗДЕЙСТВИЯ СУДОВЫХ ВОЛН НА КРЕПЛЕНИЕ ОТКОСОВ КАНАЛОВ
90. Высота расходящейся и поперечной судовой волны в канале h'c определяется по формуле
|
|
(133) |
где v - скорость движения судна в канале;
|
|
(134) |
Ω - площадь поперечного сечения канала при его расчетном, статическом уровне;
Ф - площадь подводной части миделя судна.
91. Высота судовой волны hс вблизи откоса при прохождении судна по оси канала определяется по формуле
|
|
(135) |
где В0 - ширина канала поверху при расчетном статическом уровне;
l - длина судна. При движении судна не по оси канала в формуле (135) B0 заменяется на 2.bс, где bс - расстояние судна от ближайшего откоса.
92. Длина судовой волны λс определяется по формуле
|
|
(136) |
где Н - глубина воды в канале.
В предварительных расчетах длина судовой волны может приниматься равной
|
|
(137) |
где ε принимается равным:
при ![]() ……….8.
……….8.
" ![]() …………..10.
…………..10.
93. Пологость волны ![]() принимается
приблизительно равной ε/β, но не менее 7.
принимается
приблизительно равной ε/β, но не менее 7.
Значение β принимается по формуле (134).
94. Формулы (133) - (137) могут применяться при соблюдении условий
 .
.
95. Высота наката судовой волны на откос hн.с определяется по формуле
|
|
(138) |
где k0 -принимается равным:
для бетонного покрытия откоса ………..1
» каменной облицовки ………………0,72.
96. Высота отката судовой волны с откоса ho.с, считая от расчетного статического уровня, определяется из условия
|
|
(139) |
97. Максимальное местное давление судовой волны на откос pmах определяется по формуле
|
|
(140) |
Глубина над точкой приложения давления рmах по отношению к расчетному статическому уровню определяется из условия
|
|
(141) |
98. Эпюра волнового давления на откос строится по схеме, показанной на рис. 62, где принимается:

Рис. 62. Эпюра волнового давления на откос канала
pH = 0,5pmax;
pB = 0,7pmax
99. Формулы (138) - (141) могут применяться при соблюдении условий

ПРИЛОЖЕНИЕ I
ТАБЛИЦА ОРИЕНТИРОВОЧНЫХ ПРЕДЕЛЬНЫХ РАЗГОНОВ ВОЛН
|
Наименование водоема |
Разгон волны в км |
|
Балтийское море |
375 |
|
Черное » |
500 |
|
Баренцево » Северное » Охотское » Южная часть Берингова моря Японское море |
600 |
|
Белое » |
275 |
|
Северная часть Берингова моря |
200 |
|
Океаны |
1500 |
|
Озера и водохранилища |
100 |
ПРИЛОЖЕНИЕ II
а) Метод определения давления стоячих волн в переменных Эйлера (второй порядок приближения)
В часто встречающихся случаях, когда глубина перед сооружением на водохранилищах Н ≥ 0,13λ, определение волновых воздействий может производиться следующим способом.
Расчетом определяются: фаза максимума равнодействующей; избыточное давление на статическом уровне, на дне и в любой промежуточной точке; высота подъема свободной поверхности у стенки при максимуме равнодействующей; максимальная высота подъема свободной поверхности у стенки; понижение свободной поверхности при подходе впадины волны; давление на дне и в любой промежуточной точке ниже впадины волны. По полученным значениям перечисленных параметров определяется максимальная равнодействующая давления.
Определение параметров.
Фаза максимума равнодействующей sin σ t равна
|
|
(1) |
при условии, что МR < 0 |и 2 MR| ≥ АR.
Если одно из этих условий не соблюдается, тогда sin σ t принимается равным единице.
В формуле (1)
|
|
(2) |
|
|
(3) |
Избыточное давление pz в любой точке вертикальной стенки равно
|
|
(4) |
где Aр, Вр и Ср - коэффициенты, принимаемые по табл. 1.
Таблица 1
|
Коэффициенты |
Ординаты |
Ар |
Bp |
Cp |
|
В любой точке стенки с ординатой z |
|
m[2-ch2k(H-z)] |
n-qch2k(H-z) |
|
|
На статическом |
h |
m(2-ch2kH) |
n-qch2kH |
|
|
На дне (z = H) |
|
m |
n-q |
|
Величины т, п и q (табл. 1) определяются по формулам:
|
|
(5) |
|
|
(6) |
|
|
(7) |
Высота подъема свободной поверхности zв у стенки при максимуме равнодействующей определяется по формуле
|
|
(8) |
Максимальная высота подъема свободной поверхности zгр у стенки определяется по формуле
|
|
(9) |
Понижение свободной поверхности при подходе впадины волны определяется по формуле
|
|
(10) |
б) Вспомогательные графики для определения воздействия неразбитных стоячих волн на сооружения типа вертикальной стенки (рис. 1 - 6).


Рис. 2

Рис. 3



Построение эпюры избыточного бокового давления при подходе впадины волны осуществляется путем определения давления на уровне впадины
pz вп = - γzвп
и давления на дне - по формуле (4) при
sin σ t = - 1; cos σ t = 0; cos2 σ t = - 1
Максимальная равнодействующая давления по вычисленным выше параметрам определяется из уравнения
|
|
(11) |
|
где |
(12) |
ПРИЛОЖЕНИЕ III
РАСЧЕТ ИЗМЕНЕНИЯ ПАРАМЕТРОВ ВЕТРОВЫХ ВОЛН ПРИ ПРОНИКНОВЕНИИ В ЧАСТИЧНО ЗАЩИЩЕННЫЕ ОТ ВОЛНЕНИЯ АКВАТОРИИ (рекомендуемый)
Общие положения
1. Волнение на акватории, зависящее от энергии поступающих в нее волн, определяется с учетом дифракции волн на входе в акваторию и потерь волновой энергии по пути распространения волн на акватории и по ее контуру.
В акваториях с резким изменением глубин учитывается также рефракция волн.
В качестве исходной принимается волна у входа в акваторию.
2. В зависимости от
длины волны Х, ширины входа в акваторию В (кратчайшее расстояние
между молами) и от отношения ![]() гребни и впадины волн
на акватории могут иметь в плане форму, показанную на рис. 1, а, б.
гребни и впадины волн
на акватории могут иметь в плане форму, показанную на рис. 1, а, б.
При симметричном расположении головных участков входа (молов) и нормальном подходе воли к входу главный луч волнения на акватории (линия, соединяющая точки с наибольшими высотами волн) имеет направление исходной волны.
При косом подходе волн или при несимметричных молах главный луч отклоняется от направления луча исходных волн (рис. 1, в).
3. Отклонение главного луча от направления луча исходных волн Δρ в град, определяется по формуле
|
|
(1) |
где d -проекция линии, соединяющей головы молов, на нормаль к лучу исходной волны (рис. 2);
S - проекция той же линии на луч исходной волны;
п - коэффициент, принимаемый равным;

Рис. 1
для вертикальных молов ........... 1,5
» откосных » ……………….1,75
ρ1 и ρ2 - соответственно меньший и больший углы между лучом исходных волн и осями молов в град.
Знак (-) в квадратной скобке в формуле (1) берется в случае, если на пути волны первой встречается голова мола, ось которого составляет с лучом волны меньший угол (ρ1).
Δρ всегда откладывается в сторону ρ2.
Величина Δρ может быть определена с помощью номограммы, приведенной на рис. 2, для которой формула (1) приведена к виду Δρ = n(а ± b).
4. Смещение главного луча от центра входа рекомендуется учитывать при ![]() Величина этого
смещения может быть определена по формуле
Величина этого
смещения может быть определена по формуле
|
|
(2) |

где а - угол между лучом исходной волны и линией входа;
Вп - длина части мола, перекрывающей вход (рис. 3);
т - коэффициент, принимаемый равным: для молов вертикального типа …………0,5
» »
откосного »
…………………………………………………...![]()
Знак (-) в формуле (2) принимается в случае, если мол, прикрывающий вход, составляет с лучом исходных волн меньший угол ρ1).
Величина ![]() может быть определена
также по номограмме рис. 3.
может быть определена
также по номограмме рис. 3.
Значение величины ![]() следует принимать не
более 0,5.
следует принимать не
более 0,5.
Определение волнения на акватории при дифракции волн
5. Коэффициент затухания волн с учетом дифракции и потерь энергии по пути распространения волн определяется по формуле
|
|
(3) |
где h - высота исходных воля;
h1 - высота волн в точке i акватории;
kп - коэффициент затухания за счет потерь волновой энергии, определяемый по формуле
|
|
(4) |
D - расстояние от входа акватории.
6. Коэффициент затухания волн за счет дифракции kA определяется в зависимости от B/λ:
а) при ![]()
|
|
(5) |
где А - принимается равным:
для оградительных сооружений типа вертикальной стенки
|
|
(6) |
для оградительных сооружений откосного типа
|
|
(7) |
А' - принимается равным
|
|
(8) |

Рис. 3. Номограмма для определения смещения главного луча от середины ворот порта
ρ - коэффициент, учитывающий гашение волн на откосах или стенках оградительных сооружений, определяется по формуле
|
|
(9) |
где φ1 и φ2 - внешние углы между осями оградительных сооружений и линией ворот (рис. 4,а);
D1 и D3 - соответствующие расстояния от голов оградительных сооружений до гребня волны, проходящего через точку i;
k - коэффициент, принимаемый равным:
для берегов, сложенных обломочными породами, и набросных сооружений - 0,25,
для берегов с крупной галькой и камнем - 0,17,
для Гравийных берегов и укрепленных откосов - 0,1,
для вертикальных стенок - 0,01;
q - для откосных оградительных сооружений определяется по формуле
|
|
(10) |
q - для вертикальных оградительных сооружений определяется по формуле
|
|
(11) |
где v - угол отклонения рассматриваемого луча от главного.
б) При В/λ ≥ 3
Коэффициент затухания волн kA вдоль главного луча принимается равным единице на расстоянии D0 от ворот порта, определяемом по формуле
|
|
(12) |
где ψ - Угол между лучом исходной волны и линией, соединяющей головы молов;
а - коэффициент, принимаемый равным: для молов вертикального типа 1.7
» » откосного » …………………………..1.3
D0 может также определяться по номограмме рис. 5. Коэффициент затухания волн вдоль главного луча на расстоянии D от ворот порта за пределами Do определяется по формуле
|
|
(13) |
где cρ и cλ зависимости от типа оградительных сооружений принимаются равными;
для сооружений вертикального типа
|
|
(14) |
|
|
(15) |

Рис. 4

Рис. 5. Номограмма для
определения расстояния по главному лучу ![]() (на протяжении
которого коэффициент дифракции равен 100%)
(на протяжении
которого коэффициент дифракции равен 100%)
для сооружений откосного типа
|
|
(16) |
|
|
(17) |
Величина k’д может определяться также по номограмме рис. 6.
При значениях ![]() при которых сх
становится отрицательным, в расчетах принимают cλ = 0.
при которых сх
становится отрицательным, в расчетах принимают cλ = 0.
Коэффициент затухания для боковых лучей, отклоняющихся от направления главного луча на некоторый угол v (рис. 7), определяется по формуле
|
|
(18) |
где l -принимается:
для вертикального типа оградительных сооружений
|
|
(19) |
(знак (+) принимается при определении I для большей части входа, отсекаемой главным лучом, знак (-) - для меньшей части); для откосного типа оградительных сооружений
|
|
(20) |
Величина kд может определяться также по номограмме рис. 7.
7. Коэффициент затухания волн на акватории, огражденной одиночным молом, определяется по формуле
|
|
(21) |
где ρ - угол между лучом исходных волн и направлением оси мола;
q - определяется по формулам (10) и (11).
8. Коэффициент затухания волн при полном перекрытии ворот одним из молов при заданном направлении распространения исходной волны (рис. 8) определяется в следующем порядке.
Определяется дифракция вокруг головы мола, прикрывающего вход, и определяется коэффициент затухания волн в оголовке второго мола. Затем рассчитывается дальнейшее затухание вдоль луча по направлению линии, соединяющей головы молов луча, которое принимается за направление главного луча, а также боковое затухание в обе стороны от этого луча.

Рис. 6. Номограмма для расчета коэффициентов дифракции k’д по главному лучу на акватории порта


Рис. 8. Схема полного перекрытия ворот одним из молов
Определение волнения на акватории при рефракции волн
9. Для учета влияния рефракции на волновой режим в акватории на план акватории наносятся лучи дифрагированных волн и рассматривается искривление каждого из лучей от входа до контура акватории. Изменение значений коэффициента затухания (формула (3)), за счет рефракции определяется умножением его на
![]()
где S0 - расстояние между двумя точками на лучах дифрагированных волн,
S - расстояние между этими же точками на лучах, отклоненных под влиянием рефракции.
10. Рефракция волн может определяться следующим способом.
Доопределяется
величина ![]() (где Δλ
- изменение длины волны и λср - средняя длина волны по
глубине между каждыми двумя изобатами.
(где Δλ
- изменение длины волны и λср - средняя длина волны по
глубине между каждыми двумя изобатами.
Расчет ![]() - ведется в табличной
форме для выбранных значении глубин. Сначала определяют величины H/λ затем с помощью графика рис. 17 технических
условий определяют λ
λ/λгл.
- ведется в табличной
форме для выбранных значении глубин. Сначала определяют величины H/λ затем с помощью графика рис. 17 технических
условий определяют λ
λ/λгл.
По найденным значениям λ/λгл находят Δλ/λгл между смежными изобатами и λср/λгл и по ним находят Δλ/λср.
Определение величины угла отклонения ΔΘ луча рефрагированных волн от своего первоначального положения между двумя избранными изобатами производится по номограмме (рис. 9) при угле между вол, новым лучом и нормалью к изобате Θ < 80°.
Построение диаграммы рефракции начинается с любого луча.
Прямолинейный луч дифрагированной волны продолжается до средней линии между первыми двумя прочерченными изобатами (рис. 10). В точке Pi пересечения луча со средней изобатой проводится касательная к изобате NN и измеряется угол в.
По измеренной величине Θ и известной величине λ/λср с помощью номограммы рис. 9 определяется угол ΔΘ поворота луча между первыми выбранными изобатами. Этот угол откладывается в сторону уменьшения глубины из точки P1, и новая линия луча волны прочерчивается до точки Р2, находящейся посередине между следующими двумя изобатами, для которой повторяется измерение величины угла Θ, вычисление ΔΘ и т.д.
При Θ > 80° методика построения сводится к следующему.
Измеряется расстояние l0 между изобатами в точке Р пересечения луча волны с изобатой (рис. 11).
Задаваясь величиной ![]() (где R - произвольное расстояние по направлению луча
волны) и величиной Δλ/λср между изобатами в
интервале, для которого ведется построение, по уравнению
(где R - произвольное расстояние по направлению луча
волны) и величиной Δλ/λср между изобатами в
интервале, для которого ведется построение, по уравнению
![]()
определяют величину ΔΘ, соответствующую задаваемому соотношению R/l0.
Откладывая от точки Р по направлению луча исходной
волны расстояние ![]() в найденной точке P1
поворачивают луч волны в сторону меньших глубин на угол ΔΘ, вычисленный ранее.
в найденной точке P1
поворачивают луч волны в сторону меньших глубин на угол ΔΘ, вычисленный ранее.
Измеряется в точке P1 расстояние l1 между изобатами в том интервале, в котором ведется построение, и по новому направлению луча откладывается расстояние Ri = nl1; в найденной точке Р2 вновь поворачивают луч на тот же угол ΔΘ и т.д.
Такая методика применяется до тех пор, пока угол Θ не станет меньше 80°, после чего для вычисления ΔΘ используют номограмму рис. 9.

Рис. 9. Номограмма для определения величины угла отклонения ΔΘ луча рефрагированных волн
Учет интерференции волн и местного ветрового волнения в акватории
Максимальные высоты волн в отдельных точках при интерференции двух систем волн h1 и h11 могут достигать значения
|
hинт. макс = h1 + h11 |
(22) |
При интерференции трех и более систем волн расчетная высота волны определяется наложением двух систем с наибольшими высотами волн.

Рис. 10. Рефракция волнового луча при Θ < 80°

Рис. 11. Рефракция волнового луча при Θ ≥ 80°
Высота местной ветровой волны hs определяется по формулам раздела II технических условий.
Суммарная высота волн на огражденной акватории определяется по формуле
|
|
(23) |
ПРИЛОЖЕНИЕ IV
РАСЧЕТ ПЕРЕФОРМИРОВАНИЯ БЕРЕГОВ ВОДОХРАНИЛИЩ (рекомендуемый)
Общие указания
1. Излагаемые способы расчета переформирования берегов проектируемых или эксплуатируемых водохранилищ под воздействием ветровых волн могут применяться для условий, когда первичный уклон подводного берегового склона в пределах глубины размывающего действия больше уклона устойчивой береговой отмели.
Эти способы, предусматривающие решение плоской задачи для одного выбранного профиля, в основном применимы для сравнительно прямолинейных береговых участков нижних и средних зон крупных глубоководных водохранилищ, сложенных несвязными и малосвязными грунтами. Для других грунтовых условий предусматривается введений поправочных коэффициентов на основе данных специальных исследований.
2. На характерных береговых участках водохранилищ следует проводить систематические натурные наблюдения для уточнения результатов.
Переформирование береговых склонов сложного геологического строения подлежит в каждом отдельном случае изучению с учетом всех влияющих факторов.
Примечание. К нижним
глубоководным зонам относят участки водохранилищ, глубина которых в течение
свободного от льда периода не бывает меньше ![]() к средним зонам -
мелководные озерные части водохранилища.
к средним зонам -
мелководные озерные части водохранилища.
3. Соотношение объемов аккумулятивной и абразионной частей берегового склона определяется относительным содержанием в береговых породах частиц крупностью более 0,1 мм, условиями продольного перемещения наносов и особенностями строения дна.
Упрощенная схема переформирования берегового склона изображена на рис. 1.

Рис. 1. Схема переформирования берегового склона
4. Для определения влияния продольного потока наносов на положение конечной береговой отмели и на ее развитие во времени в каждом конкретном расчетном случае учитывается наличие зон питания наносами различной крупности, форма береговой линии в плане; глубина и форма подводной части береговых склонов.
Влияние продольного потока наносов на соотношение абразионной и аккумулятивной частей склона можно учитывать введением поправочных коэффициентов аккумуляции.
Расчеты и прогнозы береговых переформирований
5. В состав расчетов переформирования берегов водохранилищ, входит:
а) расчет предельного положения береговой отмели;
б) расчет береговых переформирований, вызванных волнами заданных параметров при постоянном уровне, воды и при переменном уровне воды;
в) прогноз береговых переформирований на заданный срок.
6. За расчетную принимается высота волн 15% обеспеченности, примерно равная 0,7 высоты волны h1%, определяемой по указаниям раздела II технических условий.
Расчетный высокий уровень водохранилища назначается с учетом нагона. При отсутствии данных по нагону за расчетный принимается подпорный уровень плюс 0,5 м.
А. Расчет предельного положения береговой отмели
7. Кривая bf (рис. 1) предельного положения абразионной части отмели строится по уравнению
|
|
(1) |
где
|
|
(2) |
Величины тп и т0, представляющие собой уклон береговой отмели на урезе (тп ) и на условной глубине 10 м (т0), принимаются в зависимости от крупности частиц d, формирующих соответствующую часть отмели, по табл. 1. При этом тп определяется по крупным фракциям dn , содержащимся в размытом волнами материале, а т0 - по мелким фракциям d0.
Для определения величины dn и d0 строится кривая гранулометрического состава, характеризующая весь объем разрушения W (объем abc, рис. 1). Из всего состава фракций исключают частицы с диаметром меньше 0,1 мм; среднюю крупность из 30% наиболее мелких оставшихся фракций принимают за d0, среднюю крупность из 10% наиболее крупных фракций - за dп.
8. Глубина размывающего действия на краю береговой отмели H в м определяется по рис. 2.
Значения η/d по рис. 2 приведены в табл. 1

Рис. 2. График для определения глубины размывающего действия волн
Таблица 1
|
Вид грунта |
Крупность частиц d в мм |
тп |
т0 |
Показатель устойчивости |
|
Ил |
0,001 - 0,01 |
- |
- |
- |
|
Пыль |
0,01 - 0,1 |
0,005 |
0,001 |
100 |
|
Песок мелкий |
0,1 - 0,25 |
0,03 |
0,005 |
70 |
|
» средний |
0,2 - 0,5 |
0,07 |
0.01 |
70 |
|
» крупный |
0,5 - 1 |
0,14 |
0,02 |
70 |
|
Гравий мелкий |
1 - 2 |
0,19 |
0,03 |
45 |
|
» средний |
2 - 5 |
0,21 |
0,05 |
45 |
|
» крупный |
5 - 10 |
0,25 |
0,08 |
25 |
|
Галечник мелкий |
10 - 20 |
0,3 |
0,1 |
11 |
|
» средний |
20 - 50 |
0,36 |
0,15 |
6 |
|
» крупный |
50 - 100 |
0,4 |
0,2 |
4 |
9. Полная ширина профиля береговой отмели в плоскости уреза воды (см. рис. 1) равна
|
B = BH + Bg, |
(3) |
где BH - ширина криволинейного участка профиля отмели по горизонтали
|
|
(4) |
Вg - ширина прямолинейного участка профиля отмели
|
|
(5) |
где АH - величина сработки уровня водохранилища за безледный период.
Пользуясь формулами (1) и (4), по заданным значениям расчетной высоты волны h и кривой фракционного состава объема разрушения аbс можно построить профиль береговой отмели bfd (см. рис. 1).
Уклон подводного берегового склона tgγп (см. рис. 1) рекомендуемся принимать равным 0,5. Уклон надводного берегового склона tgγH для несвязных пород рекомендуется принимать равным 1, но не положе, чем уклон берега в естественном его состоянии.
Смещение береговой линии и положение конечного профиля береговой отмели определяются путем наложения профиля, построенного согласно пп. 7 -9, на первоначальный профиль берега так, чтобы отношение объема аккумуляции Wa (объем cde) к объему разрушения Wp (объем аbс) на рис. 1, называемое коэффициентом аккумуляции δ, было равно относительному содержанию в объеме разрушения частиц крупностью больше 0,1 мм.
Б. Расчет береговых переформирований при постоянном уровне воды:
10. Береговая отмель, развивающаяся в условиях устойчивого положения уровня воды под действием волн постоянной высоты ht (у внешнего края отмели), имеет на внешнем краю постоянную глубину Hi > определяемую по рис. 2, и ширину 6, увеличивающуюся в процессе развития отмели и стремящуюся к предельной ширине ВH [формула (4)].
Профиль развивающейся отмели строится по уравнению
|
|
(6) |
Каждому промежуточному профилю береговой отмели, определяемому шириной b, соответствует его положение относительно первоначального профиля берега.
Путем наложения ряда последовательно развивающихся профилей
(рис, 3) находится зависимость объемов разрушения ω и смещения
береговой линий I от ширины отмели b, l = > f2(b) и ω = f1(b), которая потом строится на графике. Методом конечных
разностей находится производная ![]() выражение
которой в виде ω' = f3(b) строится на том же графике.'
выражение
которой в виде ω' = f3(b) строится на том же графике.'
Примечание. Подобная же последовательность развития всей отмели, являющаяся сглаженным результатом действия многих штормов на разных уровнях, может быть принята и при наличии сработки водохранилища, т.е. при конечной форме профиля, построенной в соответствии с п. 9.
В этом случае также может быть построен график зависимости l = f1(b) и ω = f2(b), который используется в дальнейших расчетах.
В этом случае промежуточные профили, как и предельный профиль, состоят из криволинейного и прямолинейного участков, ограниченных постоянными глубинами Hi и Нi + АH.
Указанные зависимости позволяют переходить от величины ω, полученной расчетом, к форме профиля по параметру b и к положению профиля отмели относительно первоначального профиля берега по параметру l.

Рис. 3. Схема положения профиля отмели во времени
11. Время I, в течение которого ширина береговой отмели изменяется от bп до bn+1, определяется по формуле
|
|
(7) |
где N - расчетная мощность волны, принимаемая равной
|
|
(8) |
φ - угол, образованный направлением разгона волны и нормалью к береговой линии (в плане);
ε - коэффициент, определяющий сопротивляемость породы волновому воздействию. Ориентировочные значения ε для некоторых пород приведены в табл. 2.
Таблица 2
|
Характеристика пород |
Значения ε в т/м2 |
|
Плотные скальные породы, известняки, доломиты, глинистые и известковые мергели, сцементированные песчаники, очень плотные глины и алевролиты |
10000 и более |
|
То же, выветрелые и сильно трещиноватые |
7000 - 3000 |
|
То же, перемятые в виде осыпей с включением других пород |
3000 - 500 |
|
Глины плотные в ненарушенном состоянии |
5000 - 1500 |
|
То же, в нарушенном состоянии |
1500 - 150 |
|
Глины тощие в ненарушенном состоянии |
2000 - 1000 |
|
То же, в нарушенном состоянии |
500 - 100 |
|
Пески мелкозернистые сцементированные в ненарушенном состоянии |
2000 |
|
То же, в осыпи |
200 |
|
Пески мелкозернистые сильно уплотненные |
1000 - 500 |
|
То же, в осыпи |
100 - 50 |
|
Пески слабо уплотненные в ненарушенном состоянии |
200 - 100 |
|
То же, в осыпи |
100 - 50 |
|
Суглинки и супеси в ненарушенном состоянии |
1000 - 500 |
|
То же, в нарушенном состоянии |
200 - 100 |
|
Лессовидные и пылеватые суглинки в не нарушенном состоянии |
300 - 150 |
|
То же, в нарушенном состоянии |
100 - 50 |
Примечание. Уточненные расчетные значения ε устанавливаются на основании натурных и лабораторных исследований.
В расчет вводится средневзвешенное значение е. вычисленное с учетом сопротивляемости всех слоев пород, заключенных в объеме разрушения Wp. При этом принимается, что нижний слой этого объема, возвышающийся над расчетным уровнем на высоту расчетной волны, перерабатывается в ненарушенном состоянии, а вышерасположенные слои - в состоянии осыпи.
Для определения значения bi ,
соответствующего заданной продолжительности Т действия волн hi (в
дальнейших расчетах всегда Г = 12 час), формула (7) применяется для ряда
последовательных интервалов b0
- b1,
b1 - b2, b2 - b3 и т.д. до
такого последнего интервала bn-1
- bn,
для которого ![]()
В границах этого интервала значение bi находится интерполяцией. Интервалы значений b выбираются с таким расчетом, чтобы в пределах каждого интервала переменная величина ω’ могла без большой погрешности заменяться средним для этого интервала ее значением. Начальное значение b0 равно расстоянию между точкой уреза и створом, где глубина на начальном профиле равна Hi (рис. 3).
В. Расчет береговых переформирований при переменном уровне воды
12. Объем разрушения ω1, вызванного волнами одинаковой высоты hi действующими с перерывами в течение большого числа часов (в календарном исчислении годы и десятки лет) и при наличии колебания уровня в пределах безледоставной сработки водохранилища АH, можно определять по формуле
|
|
(9) |
где Wi - предельный объем разрушения, определенный способом, изложенным в пп. 6 - 9 для заданных значений hi и АH;
Xi - определяется по формуле
|
|
(10) |
Величина ω1,
соответствующая заданному времени действия волнения t1, определяется путем
последовательного наложения на первоначальный профиль берега размывов от ряда
кратковременных волнений (цикла штормов), условной продолжительностью T =
12 час. с одинаковыми волнами высотой hi и средневзвешенной
мощностью ![]() действующих на
различных уровнях воды. Выбор уровней производится в соответствии с режимом
сработки водохранилища. Размывающее действие каждого отдельного волнения
(шторма) определяется способом, изложенным в пп. 10 и 11.
действующих на
различных уровнях воды. Выбор уровней производится в соответствии с режимом
сработки водохранилища. Размывающее действие каждого отдельного волнения
(шторма) определяется способом, изложенным в пп. 10 и 11.
Для определения числа я отдельных 12-часовых волнений (числа штормов) в цикле рекомендуется формула
|
|
(11) |
с округлением до ближайшего большего целого числа.
Отметки уровней, на которых развиваются отдельные волнения (штормы), определяются разбивкой кривой обеспеченности безледоставных уровней водохранилища на я частей вертикальными равноотстоящими линиями. Чередование волнений в цикле рекомендуется устанавливать в порядке нарастания уровней от низших к высшим. В целях упрощения расчета рекомендуется объединять на общей средней отметке уровней те штормы, разность отметок которых не превышает 1 м.
Под величиной wt понимается только та часть объема разрушения от действия я волнений, которая заключена внутри контура предельного объема разрушения Wi.
Г. Прогноз береговых переформирований на заданный срок
13. Расчет прогнозирования береговых переформирований производится в следующей последовательности:
устанавливается
расчетный волновой режим для случаев, характеризуемых средними значениями hI, hII, hIII и hIV и
средневзвешенными мощностями волн ![]() и
и ![]() N}W для 12-часовых волнений, имеющих соответственно повторяемость 1, 10, 100
и 1 000 раз в течение 50 лет (по п. 14);
N}W для 12-часовых волнений, имеющих соответственно повторяемость 1, 10, 100
и 1 000 раз в течение 50 лет (по п. 14);
определяется предельное положение береговой отмели для всех указанных волнений, для которых устанавливаются: предельный объем разрушения Wi с учетом сработки водохранилища, предельная ширина криволинейного участка береговой отмели bH i и начальная ширина береговой отмели b0 i, (пп. 6 - 9);
для наибольшего волнения I находятся зависимости ω = f1(b) и l = f2(b) (п. 10);
определяется цикл штормов для волнения II (п. 12) и путем последовательного наложения этих штормов определяются величины t1 и ω1, а по ним величина ХII (пп. 11 и 12);
пользуясь формулами (10) и (16), определяют значение Xi для всех остальных волнений и строится кривая ω = f(T) для наиболее вероятных размывов;
по табл. 3 определяются зависимости ω = f(T) для объемов разрушений различной обеспеченности;
используя кривые ω = f(T), ω = f1(b) и f2(b), вычерчивают профили береговой отмели на заданные сроки прогнозирования и заданные обеспеченности.
14. Волновой режим рассматриваемого участка побережья водохранилища задается в виде кривой обеспеченности высот волн h и соответствующей этим высотам кривой средневзвешенной мощности волн N.
Кривая обеспеченности высот волн строится по данным ветрового режима водохранилища путем пересчета наблюденных скоростей ветра для румбов, обращенных в сторону водоема, в соответствующие значения высот волн.
Средневзвешенная мощность ![]() определяется
для волн заданной высоты h с учетом распределения этих волн во времени по указанным выше румбам (j)
по формуле
определяется
для волн заданной высоты h с учетом распределения этих волн во времени по указанным выше румбам (j)
по формуле
|
|
(13) |
где pj - повторяемость волн румба j, лежащих в интервале высот h + Δh и h - Δh;
Δh - произвольная достаточно малая величина.
Значения А и N находятся (аналогично рис. 4), исходя из расчета повторяемости р и обеспеченности Р волнений; повторяемость р выражается в % и вычисляется по формуле
|
|
(14) |
где i -для случаев I, II, III, IV имеет соответственно значения: 1, 10, 100 и 1000;
N - число дней в году, когда водохранилище свободно от льда.

Рис, 4
15. Объем разрушения на заданный календарный срок определяется путем суммирования действия всех учитываемых волнений различной силы (I, II, III, IV), имеющих каждое свою продолжительность (в часах), соответствующую указанному календарному сроку. Для определения этого объема используется формула, дающая суммарный объем разрушений, который получен в результате волнения hi, продолжавшегося ti час. и начавшего свое действие, когда предыдущие волнения уже разрушили берег в объеме ω0. Эта формула имеет вид
|
|
(15) |
Для упрощения расчета величина я, входящая в уравнения (9), (10), (15), определяется способом последовательного наложения штормов лишь для волнения И. Для других волнений i значение xi - может определяться приближенно по формуле
|
|
(16) |
где Wn и Wt - предельные объемы разрушения, соответствующие волнениям II и i, определяемые с учетом сработки водохранилища;
BHII и BHi - ширина криволинейного участка предельной отмели для тех же волнений;
bо II и boi - ширина начальной отмели для тех же волнений.
Расчет значения ω может производиться в следующей последовательности (в табличной форме):
|
Срок прогнозирования T лет |
Индекс волнений i |
Продолжительность волнений 1 t в час. |
Суммарная продолжительность волнений Σt в час |
Объем разрушения |
|
|
до начала волнения i ω0 |
после окончания волнения i [по формуле (15)] |
||||
|
|
|
|
|
|
|
Для каждого срока прогнозирования суммирование размывов начинается со слабых волнений (IV) и далее переходит постепенно к более сильным. Конечный размыв ωi, полученный в результате действия последнего рассматриваемого волнения, принимается за начальный объем разрушения ω0 при учете действия последующего волнения. Подобно этому и итоговый размыв всех штормов за один срок прогнозирования принимается за начальный объем разрушения при расчете на следующий срок прогнозирования.
Результат расчета дается в виде кривой зависимости ω = f(T), причем Т выражается в годах (рис. 5).
Переход от расчетного объема разрушения ω к расчетному профилю отмели и к положению профиля отмели относительно первоначального профиля берега производится, согласно указаниям п. 10, по кривым ω = f1(b) и l = f2(b), построенным для волнений I с учетом сработки водохранилища.

Рис. 5. Кривые объемов вероятных размывов
16. В результате случайных отклонений действительного Сочетания волнений от наиболее вероятного, определяемого расчетом (п. 14), могут возникать отклонения действительных объемов разрушений от наиболее вероятных. Величина возможного объема разрушения заданной обеспеченности Р на заданный срок прогнозирования Т определяется сроком ТР , в течение которого осуществляется наиболее вероятный размыв ωт.р, представленный на рис. 5 сплошной линией. Значения ТР, вычисленные на основе теории вероятности, приведены в табл. 3.
Таблица 3
Значение ТР
|
T лет |
Обеспеченность Р в % |
|||||||||
|
99 |
95 |
90 |
80 |
60 |
40 |
20 |
10 |
5 |
1 |
|
|
12,5 |
5,4 |
7,7 |
9 |
10,6 |
12,1 |
12,9 |
14,4 |
16 |
17,3 |
19,6 |
|
25 |
14,5 |
17,9 |
19,6 |
21,8 |
24,2 |
20,8 |
28,2 |
30,4 |
32,1 |
35,5 |
|
50 |
34,8 |
39,3 |
41,9 |
45 |
48,8 |
51,2 |
55 |
58,1 |
60.7 |
65,2 |
|
100 |
78,2 |
84,6 |
88,4 |
92,6 |
98,6 |
101,4 |
107,4 |
111,6 |
115.4 |
121,8 |
|
200 |
169 |
178 |
183 |
189,1 |
197,4 |
202,6 |
210,9 |
217 |
222 |
231 |
Располагая кривой зависимости наиболее вероятных размывов (рис. 5) и таблицей значений ТР, можно построить кривые объемов разрушения заданных обеспеченностей ωp Пример таких кривых приведен на рис. 5.
Прогноз береговых переформирований методом аналогии
17. При массовых расчетах прогнозирования береговых переформирований, относящихся к участкам побережья, не имеющим большого народнохозяйственного значения, может применяться метод аналогии при наличии расчетов для участков аналогов, сходных по строению берега и по гидрологическим условиям.
Метод аналогии сводится к определению для рассматриваемого участка предельного положения береговой отмели при наибольшем волнении I (см. пп. 7 -9) и к построению зависимости ω = f1(b) и l = f2(b) (п. 10),
Объем разрушения wt на заданный срок ti определяется по формуле
|
|
(17) |
где Wt и W0 - предельные объемы разрушения соответственно для рассматриваемого участка и для аналога;
ω0 - объем разрушения аналога на срок ![]() причем под ε1 и ε0 понимаются средневзвешенные значения
коэффициента сопротивляемости (табл. 2) соответственно для рассматриваемого
участка и для аналога.
причем под ε1 и ε0 понимаются средневзвешенные значения
коэффициента сопротивляемости (табл. 2) соответственно для рассматриваемого
участка и для аналога.
Переход от определенной расчетом величины ωi к соответствующему профилю отмели и к положению ее относительно первоначального берега производится по зависимостям ω = f1(b) и l = f2(b).
Упрощенный метод расчета береговых переформирований для средних зон водохранилищ
18. Объем размыва берега Q в м3 на 1 пог. м на заданный срок может определяться по формуле
|
|
(18) |
где E - расчетная среднемноголетняя энергия волнения в тм в год;
kр - показатель размываемости грунтов берегов в м3 на тм работы волн;
kб - коэффициент, учитывающий влияние высоты берега;
t - заданный срок размыва в годах;
b - показатель степени, зависящий от условий образования и отложения прибрежных осадков.
При t > 20 лет расчет рассматривается как первое приближение.
Е рассчитывается по многолетним данным наблюдений за ветрами на ближайшей гидрометеостанции. Для всех ветров, различающихся направлением и скоростью, определяется суммарная продолжительность в сутках за среднемноголетний период отсутствия льда.
Для выбранного пункта берега используются данные лишь наветренных румбов. Для этих ветров, по указаниям раздела II технических условий, определяются высоты возможных волн 1 % обеспеченности и, пользуясь графиками, тип которых изображен на рис. 6, по высоте этих волн и продолжительности действия ветров tw находят энергию данного волнения в тоннометрах.
Суммарная величина Е по наветренным румбам рассчитывается на 1 пог. м длины берега с учетом угла подхода волн.
kp определяется с учетом физико-технических свойств пород и особенностей структуры берегового откоса.
Ориентировочные значения kp:
для очень легко размываемых пород (аллювиальные мелкозернистые пески, супеси легкие пористые лессовидные) - от 0,0065 до 0,003 м3/тм;
для легко размываемых (аллювиальные разнозернистые и среднезернистые пески, делювиальные легкие суглинки пористые и рыхлые, супеси со щебнем) - от 0,003 до 0,001 м3/тм;
для пород средней размываемости (тяжелые делювиальные суглинки, ледниковые суглинки с валунами, озерные и морские глины, флювиогляциональные пески с гравием и галькой) - от 0,001 до 0,0005 м3/тм;
для трудно размываемых пород (флювиогляциальные галечники с песком и валунами, песчаники глинистые морского происхождения, морские глины с прослоями опок) - менее 0,0005 м3/тм;
Эмпирический коэффициент kб принимается равным кб = ahб,
где hб- осредненная высота берега;
a - при легко размываемых породах принимается равным 0,03, при трудно размываемых - 0,05.
При расчетах следует учесть, что при малых сроках прогнозирования вероятны большие отклонения ветров и энергии волнения от среднемноголетних.

Рис. 6
Показатель степени b, численно равный доле, которую будет занимать абразионная часть отмели от общей ее ширины, назначается в пределах 0,45 - 0,9 (п. 3).
Изложенный метод расчета позволяет определять время размыва берега по заданному предполагаемому объему размытых пород.
Определение ширины зон размыва S на заданные сроки производится графически на инженерно-геологических профилях по полученным расчетным значениям Q.
Контуры размыва подбираются по площади Q, как показано на рис. 7, для типичного профиля данного побережья с осредненной высотой h6.

Рис. 7. Схема переформирования берегового склона
Абразионная часть отмели располагается между верхним и нижним пределами размыва (ВПР и НПР), определяемыми для данной части водохранилища и данного пункта следующим способом.
Находят верхний и нижний расчетные уровни воды: по графику повторяемости - примерно 2 - 4%, по графику обеспеченности - примерно 6 и 96%. К верхнему уровню прибавляют одну треть высоты «рабочей волны», производящей в данном месте максимум размывающей работы, и от нижнего уровня откладывают вниз одну высоту рабочей волны.
Полученные графически зоны размыва распространяются на весь отрезок побережья.
При наличии преобладающего сильно выраженного косого подхода волн и продольных береговых потоков наносов зоны размыва несколько расширяются в начале данного отрезка побережья и сужаются к его концу, где скапливается наибольшее количество наносов.








































