|
ФЕДЕРАЛЬНОЕ
АГЕНТСТВО |
||
|
|
НАЦИОНАЛЬНЫЙ |
ГОСТ
Р (ИСО 12213-3:2006) |
Государственная система
обеспечения
единства измерений
ГАЗ
ПРИРОДНЫЙ.
ФАКТОР СЖИМАЕМОСТИ ГАЗОВОЙ ФАЗЫ
Метод расчетного определения
на основе данных
о физических свойствах газа
ISO 12213-3:2006
Natural gas - Calculation of compression factor -
Part 3: Calculation using physical properties
(MOD)
|
|
Москва |
Цели и принципы стандартизации в Российской Федерации установлены Федеральным законом от 27 декабря 2002 г. № 184-ФЗ «О техническом регулировании», а правила применения национальных стандартов Российской Федерации - ГОСТ Р 1.0-2004 «Стандартизация в Российской Федерации. Основные положения»
Сведения о стандарте
1 ПОДГОТОВЛЕН Федеральным государственным унитарным предприятием «Российский научно-технический центр информации по стандартизации, метрологии и оценке соответствия» (ФГУП «СТАНДАРТИНФОРМ») на основе собственного аутентичного перевода на русский язык международного стандарта, указанного в пункте 4
2 ВНЕСЕН Техническим комитетом по стандартизации ТК 180 «Государственная служба стандартных справочных данных»
3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 13 декабря 2011 г. № 1101-ст
4 Настоящий стандарт модифицирован по отношению к международному стандарту ИСО 12213-3:2006 «Газ природный. Расчетное определение фактора сжимаемости. Часть 3. Расчетное определение на основе данных о физических свойствах газа» (ISO 12213-3:2006 «Natural gas - Calculation of compression factor - Part 3: Calculation using physical properties») путем изменения его структуры для приведения в соответствие с правилами, установленными в ГОСТ Р 1.5-2004 (подразделы 4.2 и 4.3), а также путем изменения отдельных фраз (слов и ссылок), которые выделены в тексте полужирным курсивом.
Внесение указанных технических отклонений направлено на учет особенностей объекта стандартизации, характерных для Российской Федерации, а также связано с целесообразностью использования ссылочных национальных и межгосударственных стандартов вместо ссылочных международных стандартов.
Наименование настоящего стандарта изменено относительно наименования указанного международного стандарта для приведения в соответствие с ГОСТ Р 1.5-2004 (пункт 3.5).
Сопоставление структуры настоящего стандарта со структурой указанного международного стандарта приведено в дополнительном приложении ДА
5 ВВЕДЕН ВПЕРВЫЕ
Информация об изменениях к настоящему стандарту публикуется в ежегодно издаваемом информационном указателе «Национальные стандарты», а текст изменений и поправок - в ежемесячно издаваемых информационных указателях «Национальные стандарты». В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ежемесячно издаваемом информационном указателе «Национальные стандарты». Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет
СОДЕРЖАНИЕ
ГОСТ Р
8.769-2011
(ИСО 12213-3:2006)
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
|
Государственная система обеспечения единства измерений ГАЗ ПРИРОДНЫЙ. ФАКТОР СЖИМАЕМОСТИ ГАЗОВОЙ ФАЗЫ Метод расчетного определения на основе данных о физических свойствах газа State system
for ensuring the uniformity of measurements. Natural gas. |
Дата введения - 2013-01-01
1 Область применения
Настоящий стандарт устанавливает метод расчетного определения фактора сжимаемости природного газа, подготовленного для транспортирования и распределения по магистральным газопроводам, при условии его нахождения только в газовой фазе.
Стандарт распространяется на подготовленные для транспортирования по магистральным газопроводам газы в диапазонах давления и температуры, при которых на практике осуществляют транспортирование и распределение этих газов.
Более детальные сведения о применении метода изложены в [1].
2 Нормативные ссылки
В настоящем стандарте использованы нормативные ссылки на следующие стандарты:
ГОСТ Р 8.662-2009 (ИСО 20765-1:2005) Государственная система обеспечения единства измерений. Газ природный. Термодинамические свойства газовой фазы. Методы расчетного определения для целей транспортирования и распределения газа на основе фундаментального уравнения состояния AGA8 (ИСО 20765-1:2005 «Газ природный. Расчет термодинамических свойств. Часть 1. Свойства газовой фазы для транспортирования и распределения», MOD)
ГОСТ Р 8.668-2009 Государственная система обеспечения единства измерений. Теплота (энергия) сгорания объемная природного газа. Общие требования к методам измерений
ГОСТ 8.417-2002 Государственная система обеспечения единства измерений. Единицы величин
ГОСТ 31369-2008 Газ природный. Вычисление теплоты сгорания, плотности, относительной плотности, числа Воббе на основе компонентного состава (ИСО 6976-1:1995 «Газ природный. Расчет теплотворной способности, плотности, относительной плотности и индекса Вобба для смеси», MOD)
Примечание - При пользовании настоящим стандартом целесообразно проверить действие ссылочных стандартов в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет или по ежегодно издаваемому информационному указателю «Национальные стандарты», который опубликован по состоянию на 1 января текущего года, и по соответствующим ежемесячно издаваемым информационным указателям, опубликованным в текущем году. Если ссылочный стандарт заменен (изменен), то при пользовании настоящим стандартом следует руководствоваться заменяющим (измененным) стандартом. Если ссылочный стандарт отменен без замены, то положение, в котором дана ссылка на него, применяется в части, не затрагивающей эту ссылку.
3 Термины, определения и обозначения
3.1 Термины и определения
В настоящем стандарте применены термины по ГОСТ Р 8.662, ГОСТ Р 8.668, ГОСТ 8.417, ГОСТ 31369, с учетом [1].
3.2 Обозначения
3.2.1 Условные обозначения
Условные обозначения величин приведены в таблице 1.
Обозначения величин и их единиц, указанные в таблице 1, использованы как в основном тексте стандарта, так и в приложении В. Единицы величин, приведенные в таблице 1, соответствуют значениям коэффициентов, приведенным в приложении В.
Таблица 1 - Условные обозначения величин
|
Единица |
||
|
Обозначение |
Наименование |
|
|
bН0 |
Член нулевого порядка (постоянная) в разложении B11 по степеням молярной теплоты сгорания (HСН) [уравнение (В.20)] |
м3 · кмоль-1 |
|
bН1 |
Член первого порядка (линейный) в разложении B11 по степеням молярной теплоты сгорания (HСН) [уравнение (В.20)] |
м3 · МДж-1 |
|
bН2 |
Член второго порядка (квадратичный) в разложении B11 по степеням молярной теплоты сгорания (HСН) [уравнение (В.20)] |
м3 · кмоль · МДж-2 |
|
|
Члены разложения BН0 по температуре [уравнение (В.21)] |
м3 · кмоль-1 м3 · кмоль-1 · К-1 м3 · кмоль-1 · К-2 |
|
|
Члены разложения BН1 по температуре [уравнение (В.21)] |
м3 · МДж-1 м3 · МДж-1 · К-1 м3 · МДж-1 · К-2 |
|
|
Члены разложения BН2 по температуре [уравнение (В.21)] |
м3 · кмоль · МДж-2 |
|
м3 · кмоль · МДж-2 · К-1 |
||
|
м3 · кмоль · МДж-2 · К-2 |
||
|
|
Члены разложения Bij по температуре [уравнение (В.22)] |
м3 · кмоль-1 |
|
м3 · кмоль-1 · К-1 |
||
|
м3 · кмоль-1 · К-2 |
||
|
B |
Второй вириальный коэффициент [уравнение (1)] |
м3 · кмоль-1 |
|
Bij |
Второй вириальный коэффициент парного взаимодействия между компонентом i и компонентом j [уравнение (В.22)] |
м3 · кмоль-1 |
|
cН0 |
Член нулевого порядка (постоянный) в разложении С111 по степеням молярной теплоты сгорания (HСН) [уравнение (В.29)] |
м6 · кмоль-2 |
|
cН1 |
Член первого порядка (линейный) в разложении С111 по степеням молярной теплоты сгорания (HСН) [уравнение (В.29)] |
м6 · кмоль-1 · МДж-1 |
|
cН0 |
Член нулевого порядка (постоянный) в разложении С111 по степеням молярной теплоты сгорания (HСН) [уравнение (В.29)] |
м6 · кмоль-2 |
|
cН1 |
Член первого порядка (линейный) в разложении С111 по степеням молярной теплоты сгорания (HСН) [уравнение (В.29)] |
м6 · кмоль-1 · МДж-1 |
|
cН2 |
Член второго порядка (квадратичный) в разложении С111 по степеням молярной теплоты сгорания (HСН) [уравнение (В.29)] |
м6 · МДж-2 |
|
|
Члены разложения cН0 по температуре [уравнение (В.30)] |
м6 · кмоль-2 |
|
м6 · кмоль-2 · К-1 |
||
|
м6 · кмоль-2 · К-2 |
||
|
|
Члены разложения cН1 по температуре [уравнение (В.30)] |
м6 · кмоль-1 · МДж-1 |
|
м6 · кмоль-1 · МДж-1 · К-1 |
||
|
м6 · кмоль-1 · МДж-1 · К-2 |
||
|
|
Члены разложения cН2 по температуре [уравнение (В.30)] |
м6 · МДж-2 |
|
м6 · МДж-2 · К-1 |
||
|
м6 · МДж-2 · К-2 |
||
|
|
Члены разложения cijk по температуре [уравнение (В.31)] |
м6 · кмоль-2 |
|
м6 · кмоль-2 · К-1 |
||
|
м6 · кмоль-2 · К-2 |
||
|
C |
Третий вириальный коэффициент [уравнение (1)] |
м6 · кмоль-2 |
|
Cijk |
Перекрестный третий вириальный коэффициент [уравнение (В.31)] |
м6 · кмоль-2 |
|
D |
Относительная плотность [d (воздух) = 1; уравнение (В.1)] |
1 |
|
DHСН |
Изменение молярной теплоты сгорания HСН во время итераций [уравнения (В.10) и (В.11)] |
МДж · кмоль-1 |
|
HS |
Значение высшей теплоты сгорания [газ при нормальных условиях (0 °C, 1013 25 бар), температура сгорания 25 °C] |
МДж · м-3 |
|
H |
Молярная теплота сгорания (температура сгорания 25 °C) |
МДж · кмоль-1 |
|
M |
кг · кмоль-1 |
|
|
P |
Абсолютное давление |
бар* |
|
R |
Универсальная газовая постоянная |
м3 · бар · кмоль-1 · К-1 |
|
T |
Абсолютная температура |
K |
|
t |
Температура в градусах Цельсия [t = T - 273,15; уравнение (В.27)] |
°C |
|
U |
Относительная расширенная неопределенность |
% |
|
Vm |
Молярный объем (= 1/ρm) |
м3 · кмоль-1 |
|
X |
Молярная доля компонента |
1 |
|
Y |
Комбинационные параметры для перекрестных вторых вириальных коэффициентов B12 и B13 (таблица В.2) и перекрестных третьих вириальных коэффициентов Cijk [уравнение (В.32)] |
1 |
|
Z |
Фактор сжимаемости |
1 |
|
ρ |
кг · м-3 |
|
|
ρm |
Молярная плотность
(= |
кмоль · м-3 |
|
* Несмотря на то что бар не относится к системным единицам, применяемый международный стандарт ориентирован на использование в расчетах (в том числе в компьютерной версии) этой единицы (1 бар = 0,1 МПа). По этой причине в настоящем стандарте давление, включая давление для универсальной газовой постоянной R, может быть выражено в единице «бар» или единице «МПа» в зависимости от того, как данные единицы представлены в различных разделах применяемого международного стандарта. |
||
n - значение при нормальных условиях (Тn = 273,15 К, Рn = 0,101325 МПа);
CH - для эквивалентного углеводорода;
CO - для моноксида углерода;
CO2 - для диоксида углерода;
H2 - для водорода;
N2 - для азота.
3.2.3 Дополнительные обозначения
(air) - для сухого воздуха стандартного состава [уравнение (В.1)];
(D) - для условного значения ρ, используемого в уравнении (В.11);
1 - для эквивалентного углеводорода [уравнения (В.12) и (В.15)];
2 - для азота [уравнения (В.12) и (В.16)];
3 - для диоксида углерода [уравнения (В.12) и (В.17)];
4 - для водорода [уравнения (В.12) и (В.18)];
5 - для моноксида углерода [уравнения (В.12) и (В.19)];
(id) - состояние идеального газа;
(u) - счетчик итераций (В.2.1);
(v) - счетчик итераций (В.2.2);
(w) - счетчик итераций (В.4).
4 Метод расчетного определения
4.1 Сущность метода
Принцип метода настоящего стандарта основан на том, что для расчетного определения термических свойств подлежащего транспортированию по газопроводу природного газа достаточно информации о ряде его физических свойств. Соответствующие данные совместно с температурой и плотностью, характеризующими состояние газа, составляют комплекс входных переменных для рассматриваемого метода.
В методе используют следующие физические свойства: высшую теплоту сгорания, относительную плотность и молярную долю диоксида углерода. Метод, как правило, применяют при отсутствии сведений о полном компонентном составе газа. Для газов с синтетическими примесями (синтез-газ) необходимо иметь дополнительные сведения о молярной доле водорода.
4.2 Уравнение состояния SGERG-88
Расчетный метод основан на стандартном вириальном уравнении состояния природного газа GERG-88 (SGERG-88) (источники см. в ГОСТ Р 8.662). Вириальное уравнение состояния GERG-88 получено из базового уравнения состояния GERG-88 (MGERG-88), основанного на наличии сведений о полном компонентном составе газа (источники см. в ГОСТ Р 8.662).
Фактор сжимаемости Z получают из уравнения SGERG-88 согласно уравнению
где B и C - функции входных переменных: высшей теплоты сгорания HS, относительной плотности d, молярных долей диоксида углерода и водорода (CO2 и H2) и температуры T;
ρm - молярная плотность согласно выражению
ρm = p/(ZRT), (2)
где
![]() . (3)
. (3)
При этом в методе SGERG-88 смесь природного газа рассматривают, по существу, как пятикомпонентную смесь, включающую в себя эквивалентный углеводородный газ (с теми же термодинамическими свойствами, какими обладает сумма присутствующих углеводородов), азот, диоксид углерода, водород и моноксид углерода. Для адекватного представления термодинамических свойств углеводородного газа необходимо знать также теплоту сгорания HСН. Поэтому для вычисления Z используют зависимость
Для
моделирования смесей типа коксового газа учитывают молярную долю в
фиксированном соотношении с содержанием водорода. Если водород отсутствует (![]() ), то принимают
), то принимают ![]() . Далее смесь
природного газа рассматривают в методе вычислений как трехкомпонентную смесь
(см. приложение В).
. Далее смесь
природного газа рассматривают в методе вычислений как трехкомпонентную смесь
(см. приложение В).
Вычисления проводят в три стадии с помощью итеративных операций, детально описанных в приложении В. Для исходных данных требуется смоделировать пятикомпонентную смесь, для которой могут быть с удовлетворительной точностью определены заданные значения высшей теплоты сгорания и относительной плотности.
Во-вторых, если эта модель определена, могут быть найдены B и C при использовании уравнений, также приведенных в приложении В.
На третьей стадии решают систему уравнений (1) и (2) для ρm и Z подходящим численным методом.
4.3 Входные переменные
4.3.1 Предпочтительный набор входных переменных
В качестве предпочтительных входных переменных в уравнении SGERG-88 используют абсолютное давление, температуру и высшую теплоту сгорания (в объемных единицах), относительную плотность, молярную долю диоксида углерода и водорода.
Таким
образом, в качестве входных переменных используют набор данных A: HS, d, ![]() и
и ![]() . Относительную
плотность относят к нормальным условиям p = (101,325 кПа
и t
=
0 °C), а высшую теплоту сгорания - к нормальным условиям (р = 101,325
кПа и t = 0 °C) и к
температуре вспышки t = 25 °C.
. Относительную
плотность относят к нормальным условиям p = (101,325 кПа
и t
=
0 °C), а высшую теплоту сгорания - к нормальным условиям (р = 101,325
кПа и t = 0 °C) и к
температуре вспышки t = 25 °C.
4.3.2 Альтернативные наборы входных переменных
При применении стандартного уравнения состояния GERG-88 допускается использовать альтернативные (по отношению к описанному в 4.3.1) наборы входных переменных:
![]() , HS, d и
, HS, d и![]() (набор В);
(набор В);
![]() ,
, ![]() , d и
, d и![]() (набор С);
(набор С);
![]() ,
, ![]() , HS и
, HS и![]() (набор D).
(набор D).
Использование альтернативных наборов входных переменных приводит к результатам, которые могут различаться в четвертом десятичном знаке. В настоящем стандарте рекомендовано использовать набор входных переменных А.
4.4 Условия применения метода
4.4.1 Газ, подготовленный для транспортирования и распределения по магистральным газопроводам
Для такого газа условия применения метода следующие:
- абсолютное давление: 0 МПа £ p £ 12 МПа;
- температура: 263 К £ Т £ 338 К;
-
молярная доля диоксида углерода: ![]() ;
;
-
молярная доля водорода: ![]() ;
;
- высшая теплота сгорания: 30 МДж · м-3 £ HS £ 45 МДж · м-3;
- относительная плотность: 0,55 £ d £ 0,80.
Молярные доли других компонентов природного газа не требуется рассматривать как входные переменные. Тем не менее молярные доли этих компонентов могут находиться в следующих пределах (типичное отношение молярных долей последовательных компонентов в гомологических рядах алканов 3:1 - см. приложение А):
|
- метан |
|
|
- азот |
|
|
- этан |
|
|
- пропан |
|
|
- бутаны |
|
|
- пентаны |
|
|
- гексаны |
|
|
- гептаны |
|
|
- октаны плюс высшие углеводороды |
|
|
- моноксид углерода |
0 £ хСО £ 0,03; |
|
- гелий |
0 £ xHe £ 0,005; |
|
- вода |
|
Метод применим только к смесям, находящимся в однофазном газовом состоянии (выше температуры конденсации) при заданных температуре и давлении. Для газа, подготовленного для транспортирования и распределения по магистральным газопроводам, метод применим при расширенных диапазонах температуры и давления, однако неопределенность расчетных значений при этом возрастает (см. рисунок 1). При компьютерной реализации метода нижний температурный предел устанавливают 250 К.
4.4.2 Расширенные условия применения метода
Условия применения метода, расширенные по отношению к указанным в 4.4.1, приведены ниже:
|
- абсолютное давление |
0 Мра £ ρ £ 12 МПа; |
|
- температура |
263 К £ T £ 338 К; |
|
- молярная доля диоксида углерода |
|
|
- молярная доля водорода |
|
|
- высшая теплота сгорания |
20 МДж · м-3 £ HS £ 48 МДж · м-3; |
|
- относительная плотность |
0,55 £ d £ 0,90. |
Для допустимых значений молярных долей прочих основных компонентов природного газа устанавливают интервалы:
|
- метан |
|
|
- азот |
|
|
- этан |
|
|
- пропан |
|
Интервалы значений молярных долей прочих второстепенных компонентов не изменяют по отношению к приведенным в 4.4.1 для газа, подготовленного для транспортирования по магистральным газопроводам.
Метод не разрешается применять за пределами этих интервалов; в компьютерной реализации метода, описанной в приложении В, не допускается выход за установленные пределы молярных долей.
4.5 Оценка неопределенности вычислений
Относительная
расширенная неопределенность вычислений фактора сжимаемости UZ (для
температуры от 263 К до 338 К) составляет ±0,1
% при давлении вплоть до 10 МПа и ±0,2
% между 10 и 12 МПа для природных газов типов: ![]() ,
, ![]() ,
, ![]() и
и ![]() и при 30 МДж · м-3
£ HS £ 45 МДж · м-3
и 0,55 £ d £ 0,80 (см.
рисунок 1).
и при 30 МДж · м-3
£ HS £ 45 МДж · м-3
и 0,55 £ d £ 0,80 (см.
рисунок 1).
Для газов с молярной долей СO2, превышающей 0,09, неопределенность составляет ±0,1 % при давлении вплоть до 6 МПа и при температуре от 263 K до 338 K. Оценка неопределенности выполнена на основании сравнения с результатами измерений фактора сжимаемости, приведенными в GERG - банком данных (см. библиографию в ГОСТ Р 8.662).
4.5.2 Оценка неопределенности для расширенных условий применения
Оценка расширенной неопределенности расчетных значений фактора сжимаемости, выходящей за показатели точности, приведенные в 4.5.1, рассмотрена в приложении Е.
4.5.3 Учет неопределенностей входных переменных
В таблице 2 приведены типичные оценки неопределенности соответствующих входных переменных. Эти оценки могут быть получены при оптимальных производственных условиях.
Ориентировочно, на основе анализа распределения ошибок, допускается полагать, что указанные неопределенности во входных переменных могут привести к дополнительной расширенной неопределенности расчетных результатов приблизительно ±0,1 % при давлении 6 МПа при температуре от 263 до 338 K. Свыше 6 МПа дополнительная неопределенность больше и увеличивается примерно прямо пропорционально давлению.
4.5.4 Опубликование результатов
Вычисленные значения фактора сжимаемости необходимо публиковать с четырьмя значащими цифрами в мантиссе при условиях, оговоренных в настоящем стандарте для рекомендуемого метода (уравнение состояния SGERG-88).
Уравнение состояния SGERG-88
p - давление; Т -
температура; 1 - UZ £
± 0,1
%; 2 - UZ
от ±
0,1 % до ± 0,2 %; 3 - UZ от ± 0,2 % до ±
0,5 %;
4 - UZ
от ±
0,5 % до ± 3,0 % (представленные пределы
расширенной неопределенности ожидаются
реальными для природных газов и аналогичных
газов типов: ![]() ,
, ![]() ,
, ![]() и
и
![]() при 30 МДж · м-3 £
HS
£ 45 МДж · м-3 и 0,55 £
d £
0,80)
при 30 МДж · м-3 £
HS
£ 45 МДж · м-3 и 0,55 £
d £
0,80)
Рисунок 1 -
Пределы расширенной неопределенности при вычислении
фактора сжимаемости
Таблица 2 - Неопределенности входных переменных
|
Абсолютная неопределенность |
|
|
Абсолютное давление |
±0,02 МПа |
|
Температура |
±0,15 К |
|
Молярная доля диоксида углерода |
±0,002 |
|
Молярная доля водорода |
±0,005 |
|
Относительная плотность |
±0,0013 |
|
Высшая теплота сгорания |
±0,06 МДж · м-3 |
5 Программное обеспечение метода
Программное обеспечение метода может быть предоставлено на предварительно обусловленных началах.
Приложение А
(справочное)
Газ, подготовленный для транспортирования и распределения по магистральным газопроводам
А.1 Максимальные пределы для молярных долей компонентов
Расчетный метод SGERG-88 представляет собой упрощение метода MGERG-88, для которого требуется полный компонентный состав (от СН4 до С8Н18, N2, СO2 и, при наличии, Н2 и СО), чтобы рассчитать фактор сжимаемости или плотность. Настоящий стандарт определяет соответствующие максимальные пределы молярных долей конкретных компонентов для метода SGERG-88 (см. таблицу А.1). Во второй графе таблицы А.1 указана установленная экспериментально область применения по предельному содержанию компонента, в третьей графе приведены максимальные молярные доли для природного газа, подготовленного к транспортированию по магистральным газопроводам, а в четвертой графе представлены расширенные диапазоны применения. Диапазон молярных долей компонентов природного газа с экспериментально определенными значениями фактора сжимаемости меньше, чем этот диапазон для природного газа, подготовленного к транспортированию по магистральным газопроводам, а также меньше, чем для расширенных областей применения. Для давлений до 10 МПа при значениях молярных долей компонентов в пределах составов, указанных во второй графе, экспериментальные значения из банка данных GERG воспроизводятся с расширенной неопределенностью 0,1 % (с 95 %-ной вероятностью).
Таблица А.1 - Области применения метода SGERG-88 (максимальные пределы молярных долей компонентов)
|
Область применения, проверенная экспериментально (см. рисунок 1) |
Предельное значение для природного газа, подготовленного для транспортирования по магистральным газопроводам (см. 4.4.1) |
Расширенная область применения (см. 4.4.2) |
|
|
N2 |
0,20 |
0,20 |
0,50 |
|
CO2 |
0,09 |
0,20 |
0,30 |
|
C2H6 |
0,10 |
0,10 |
0,20 |
|
C3H8 |
0,035 |
0,035 |
0,05 |
|
C4H10 |
0,015 |
0,015 |
0,015 |
|
H2 |
0,10 |
0,10 |
0,10 |
В настоящем стандарте используют термин «природный газ, подготовленный для транспортирования и распределения по магистральным газопроводам» (см. ГОСТ Р 8.662), чтобы описать природные газы, как правило, распределяемые через газопроводы (см. таблицу А.1, третья графа).
Для этих природных газов максимальный предел молярной доли диоксида углерода определен как 0,20. Однако для такого содержания CO2 значение расширенной неопределенности, равное 0,1 %, наблюдают только до давления 6 МПа (см. 4.5.1).
А.2 Проверка на согласованность и спецификация входных переменных
Для
метода SGERG-88 [как
обязательное требование по приложению В (раздел В.5)]
проводят проверку на согласованность входных переменных d, ![]() ,
, ![]() и
и ![]() .
.
В настоящем стандарте и в различных публикациях о методе SGERG-88 отмечается, что он получен для природных газов, с учетом взаимозависимостей по содержанию более тяжелых углеводородов, типичных для природных газов. Это означает в действительности, что отношение молярных долей последовательных компонентов в алкановом гомологическом ряду, как правило, 3:1. Это эмпирическое правило было доказано путем сравнения со значениями из банка данных GERG.
На
рисунках А.1
и А.2,
соответственно, приведены значения молярных долей ![]() и
и ![]() как функции молярной
доли этана
как функции молярной
доли этана ![]() для природных газов, взятых из банка
данных GERG. Точки в виде
окружностей соответствуют природному газу, подготовленному для
транспортирования по магистральным газопроводам, представленному в таблице А.1.
Для обоих наборов молярных долей это дает диапазон значений, в пределах
которого метод SGERG-88 может быть всегда применен
безопасно. Пунктирные линии на рисунках А.1 и А.2 иллюстрируют правило одной
трети для отношений молярных долей с 0,3 для
для природных газов, взятых из банка
данных GERG. Точки в виде
окружностей соответствуют природному газу, подготовленному для
транспортирования по магистральным газопроводам, представленному в таблице А.1.
Для обоих наборов молярных долей это дает диапазон значений, в пределах
которого метод SGERG-88 может быть всегда применен
безопасно. Пунктирные линии на рисунках А.1 и А.2 иллюстрируют правило одной
трети для отношений молярных долей с 0,3 для ![]() /
/![]() и 0,1 для
и 0,1 для ![]() /
/![]() . Ограничивающие
линии с обеих сторон пунктира показывают диапазон ±0,01 для молярной доли пропана и ± 0,003 для молярной доли бутана+
соответственно, в пределах которого фактически могут быть найдены все значения
молярной доли из базы данных GERG. Представление данных с использованием
абсолютных пределов допуска предпочтительнее, чем с использованием
относительных пределов допуска.
. Ограничивающие
линии с обеих сторон пунктира показывают диапазон ±0,01 для молярной доли пропана и ± 0,003 для молярной доли бутана+
соответственно, в пределах которого фактически могут быть найдены все значения
молярной доли из базы данных GERG. Представление данных с использованием
абсолютных пределов допуска предпочтительнее, чем с использованием
относительных пределов допуска.
![]() - молярная доля пропана;
- молярная доля пропана; ![]() - молярная
доля этана; 1 - газ 03-4605 (газ Северного моря - см. текст)
- молярная
доля этана; 1 - газ 03-4605 (газ Северного моря - см. текст)
Рисунок
А.1 - Молярная доля пропана для природных газов как функция
молярной доли этана
![]() - молярная доля компонентов
бутана+;
- молярная доля компонентов
бутана+;
![]() -
молярная доля этана; 1 - газ 03-4605 (газ Северного моря - см. текст)
-
молярная доля этана; 1 - газ 03-4605 (газ Северного моря - см. текст)
Рисунок А.2 -
Молярная доля бутана+ для природных газов как функция
молярной доли этана
Там, где природный газ включает в себя молярные доли компонентов, которые не входят в диапазоны, указанные на рисунках А.1 и А.2, рекомендуется проверить применимость метода SGERG-88 сравнением с другими уравнениями состояния, при использовании которых, однако, для получения результатов надлежащего качества потребуются данные о полном компонентном составе.
В качестве одного из таких примеров (газ Северного моря, условно определяемый как 03-4605, содержащий 0,0902 молярной доли этана, 0,0035 молярной доли пропана и 0,00016 молярной доли бутанов, - см. заштрихованный квадрат на рисунках А.1 и А.2), было приведено много сравнительных вычислений по другим уравнениям состояния. В этом случае в методе SGERG-88 выявлены отклонения до +0,5 % при давлении 10 МПа и температуре от 275 до 280 К.
Измерения, проведенные в системе измерения плотности газа на тех же самых изотермах, показывают, что экспериментальные значения плотности согласуются со значениями плотности, вычисленными методом, требующим знания полного компонентного состава в пределах полной неопределенности 0,04 % результатов измерений, и поэтому метод SGERG-88 признан неподходящим в этом частном нетипичном случае. Полная неопределенность результатов измерений состоит в равной степени из неопределенности результатов измерения плотности и молярных долей компонентов исследованного образца природного газа.
Там, где метод SGERG-88 не должен быть использован, рекомендуется использовать метод AGA8-DC92 (см. ГОСТ Р 8.662) или уравнение состояния GERG-2004, но эти варианты применимы только при известном полном компонентном составе природного газа.
Приложение B
(обязательное)
Описание метода расчета на основе уравнения состояния SGERG-88
В настоящем приложении приведены уравнения и числовые значения коэффициентов, которые полностью определяют SGERG - метод расчета фактора сжимаемости.
В настоящем приложении приведены также итерационные процедуры, принятые в GERG и представленные в подпрограмме SGERG.FOR, написанной на языке FORTRAN 77. По этой подпрограмме осуществляют тестовое решение; другие вычислительные процедуры могут быть приемлемыми при условии, что они приводят к таким же числовым результатам. Результаты расчетов по настоящему приложению должны совпадать с результатами, приведенными в приложении С, по крайней мере до четвертого знака после запятой. Ниже перечислены другие версии программной реализации метода, которые могут приводить к идентичным результатам:
a) версия в BASIC, описанная в GERG TM5, которая может быть использована с различными стандартными условиями. Эта программа предназначена в основном для компьютерных приложений;
b) версия в приложении С, описанная в немецких DVGW - директивах, раздел G486;
c) версия в Turbo Pascal.
Все эти программы были проверены с целью получить одинаковые результаты в пределах 10-5. Программы и условия их применения рассмотрены в [1].
В.1 Основная структура расчетного метода
Согласно разделу 4.2 расчет проводят в три этапа, которые схематически показаны на рисунке В.1.
Рисунок
В.1 - Блок-схема для стандартного расчетного метода GERG-88
(хi - молярная доля компонента i)
Расчеты выполняют в три этапа:
Этап 1
В качестве входных переменных используют давление, температуру, высшую теплоту сгорания, относительную плотность и молярные доли диоксида углерода и водорода. Если значения первых трех параметров выражены в любых других единицах, кроме [бар], [°C] и [МДж/м3], то их следует сначала преобразовать в значения в единицах [бар], [°C] и [МДж/м3], соответственно согласно требованиям приложения D.
Входные переменные затем используют для расчета следующих промежуточных данных:
- молярной доли:
- углеводородного газа xCH,
- азота ![]() ,
,
- моноксида углерода хCO,
- молярной теплоты сгорания эквивалентного углеводорода HCH;
- молярной массы эквивалентного углеводорода MCH;
- второго вириального коэффициента (Tn = 273,15 K) Bn;
- молярной плотности при нормальных условиях ρm,n;
- массовой плотности при нормальных условиях ρn;
- высшей теплоты сгорания газа HS.
В уравнениях (В.1) - (В.46) каждое обозначение представляет собой физическую величину, деленную на такую величину (см. приложение А), что их отношение является безразмерной величиной.
Этап 2
Промежуточные данные используют для расчета второго и третьего вириальных коэффициентов природного газа при данной температуре В(Т, HCH, хi) и C(Т, HCH, хi).
Этап 3
Значения второго и третьего вириальных коэффициентов, определяемых на втором этапе, подставляют в вириальное уравнение и для заданных давления и температуры рассчитывают фактор сжимаемости Z.
Используемые символы определены в 3.2.
В.2 Расчет промежуточных результатов
Промежуточные
результаты для восьми величин (xCH, ![]() , xCO, НCH, HCH, Bn, ρm,n, ρn) определяют из
уравнений (В.1)
- (В.8) с
использованием итерационного метода, представленного
на рисунке В.2 (значения констант,
используемых в этих
уравнениях, приведены в таблице В.1.):
, xCO, НCH, HCH, Bn, ρm,n, ρn) определяют из
уравнений (В.1)
- (В.8) с
использованием итерационного метода, представленного
на рисунке В.2 (значения констант,
используемых в этих
уравнениях, приведены в таблице В.1.):
ρn = dρn(air); (B.1)
![]() (В.2)
(В.2)
![]() (B.3)
(B.3)
![]() (B.7)
(B.7)
Рисунок В.2 - Блок-схема вычисления промежуточных данных с помощью итераций
Таблица В.1 - Значения констант, используемых в уравнениях (В.1) - (В.8) (приведенных в соответствие с молярной массой и молярной теплотой сгорания в ГОСТ 31369)
|
= 285,83 |
МДж · кмоль-1 |
|
|
HCO |
= 282,98 |
МДж · кмоль-1 |
|
|
= 28,0135 |
кг · кмоль-1 |
|
|
= 44,010 |
кг · кмоль-1 |
|
|
= 2,0159 |
кг · кмоль-1 |
|
MCO |
= 28,010 |
кг · кмоль-1 |
|
R |
= 0,0831451 |
м3 · бар · кмоль-1 · К-1 |
|
Vm,n(id) |
= 22,414097 |
м3 · кмоль-1 |
|
ρn(air) |
= 1,292923 |
кг · м-3 |
B.2.1 Итерация с молярной теплотой сгорания НCH (внутренний цикл)
Уравнения (В.1) - (В.8) применяют последовательно так, чтобы получить первое приближение на i-м шаге итерации.
Начальные приближения:
HCH(и = 0) = 1000 МДж · кмоль1;
Bn(v = 0) = -0,065 м3 · кмоль-1.
Значения других констант, используемых в уравнениях (В.1) - (В.8), приведены в таблице В.1. Критерий сходимости для этого внутреннего итерационного цикла такой, что абсолютная разница между расчетной плотностью газа при нормальных условиях ρn(u) и принятой плотностью (либо измеренной непосредственно, либо определенной из относительной плотности) газа при нормальных условиях ρn менее чем 10-6, т.е.
|ρn - ρn(u)| < 10-6. (В.9)
Если это условие не выполнено, то уточненное значение молярной теплоты сгорания HCH(u) для использования в уравнениях (В.5) - (В.8) рассчитывают с помощью уравнения (В.10) следующим образом:
HCH(u) = HCH(u - 1) + DHCH(u), (В.10)
где
DHCH(u) = [ρn - ρn(u)][ρ(D) - ρn(u)]-1; (B.11)
ρn(u) - значение плотности для текущего шага итерации [начиная с HCH(u - 1)],
ρn(D) - значение плотности, определяемое с помощью уравнений (В.4) - (В.8) с использованием [HCH(u - 1) + 1] в качестве исходного значения для молярной теплоты сгорания.
Когда левая часть уравнения (В.9) становится менее 10-6, итерационный цикл завершают и начинают итерации со вторым вириальным коэффициентом.
B.2.2 Итерации с использованием второго вириального коэффициента Bn (внешний цикл)
Промежуточные
значения xCH(u), ![]() , xCO и HCH(и),
полученные на предыдущих итерациях, и входные переменные
, xCO и HCH(и),
полученные на предыдущих итерациях, и входные переменные ![]() и
и ![]() используют для
определения уточненного значения второго вириального коэффициента Bn(v) для газа при
нормальных условиях.
используют для
определения уточненного значения второго вириального коэффициента Bn(v) для газа при
нормальных условиях.
Второй вириальный коэффициент для природного газа определяют по следующей формуле
Отсутствие в уравнении (В.12) членов, содержащих B25, B34 и т.д., не снижает точность расчета, поэтому они исключены из уравнения.
Bn(v) = B(Tn), (B.13)
где
T = Tn = 273,15; (В.14)
x1 = xCH(u); (В.15)
x5 = x00; (В.19)
где коэффициенты bH0, bH1 и bH2 - полиномы второй степени по отношению к температуре.
а вторые вириальные коэффициенты B14, B15, B22, B23, B24, B33, B34, B44 и B55 - также полиномы второй степени по отношению к температуре:
Перекрестные вириальные коэффициенты B12 и B13 имеют вид:
B12 = [0,72 + 1,875 · 10-5(320 - T)2](B11 + B22)/2; (В.23)
B13 = -0,865(B11 · B33)1/2. (В.24)
Коэффициенты в уравнениях (В.21) - (В.24) приведены в таблице В.2.
Таблица В.2 - Числовые значения коэффициентов b(0), b(1) и b(2) в температурном разложении второго вириального коэффициента для чистых газов и перекрестных вириальных коэффициентов (единица величины B - м3 · кмоль-1, если температуру измеряют в Кельвинах)
|
ij |
b(0) |
b(1) |
b(2) |
|
|
CH |
Н0 |
-425468 · 10-1 |
286500 · 10-3 |
-462073 · 10-6 |
|
CH |
H1 |
877118 · 10-4 |
-556281 · 10-6 |
881510 · 10-9 |
|
CH |
Н2 |
-824747 · 10-7 |
431436 · 10-9 |
-608319 · 10-12 |
|
N2 |
22 |
-144600 · 10-1 |
740910 · 10-4 |
-911950 · 10-7 |
|
CO2 |
33 |
-868340 · 10-1 |
403760 · 10-3 |
-516570 · 10-6 |
|
Н2 |
44 |
-110596 · 10-3 |
813385 · 10-5 |
-987220 · 10-8 |
|
KO |
55 |
-130820 · 10-1 |
602540 · 10-4 |
-644300 · 10-7 |
|
CH + N2 |
12 |
y = 0,72 + 1875 · 10-5(320 - T)2 |
||
|
CH + CO2 |
13 |
y = -0,865 |
||
|
СН + Н2 |
14 |
-521280 · 10-2 |
271570 · 10-4 |
-250000 · 10-7 |
|
СН + СО |
15 |
-687290 · 10-2 |
-239381 · 10-6 |
518195 · 10-7 |
|
N2 + СO2 |
23 |
-339693 · 10-1 |
161176 · 10-3 |
-204429 · 10-6 |
|
N2 + H2 |
24 |
120000 · 10-2 |
0,00000 |
0,00000 |
Значение Bn(v), полученное из уравнения (В.13), применяют для расчета v-го приближения ρm,n с использованием уравнения (В.4).
Уравнение (В.6) затем используют с другой целью, в отличие от той, для которой оно было использовано ранее, т.е. с целью получить значения HS(v):
HS(v) = [x1(u)HCH(u - 1) + x4 · H4 + x5H5]ρm,n(v), (B.25)
где
![]() и H5 (= HCO) - молярная
теплота сгорания при температуре 298,15 К для водорода и моноксида углерода
соответственно. Критерий сходимости для внешнего итерационного цикла (счетчик
итераций v) означает то,
что абсолютная разность между измеренным значением высшей теплоты сгорания HS и ее расчетным
значением HS(v) должна быть
менее 10-4, т.е.
и H5 (= HCO) - молярная
теплота сгорания при температуре 298,15 К для водорода и моноксида углерода
соответственно. Критерий сходимости для внешнего итерационного цикла (счетчик
итераций v) означает то,
что абсолютная разность между измеренным значением высшей теплоты сгорания HS и ее расчетным
значением HS(v) должна быть
менее 10-4, т.е.
|HS - HS(v)| < 10-4. (B.26)
Если этот критерий будет удовлетворен, то значение Bn(v), определенное из уравнения (В.13), используют в качестве нового входного значения для уравнения (В.4), и полную итерационную процедуру, то есть внутренний итеративный цикл (счетчик итераций u), повторяют, начиная с уравнения (В.5), используя при этом текущие значения HCH(u - 1) и ρm,n(v).
Когда
будут удовлетворены одновременно критерии сходимости (В.9) и (В.26),
получают конечные промежуточные значения для молярных концентраций xCH и ![]() и молярной
теплоты сгорания HCH.
и молярной
теплоты сгорания HCH.
В.3 Расчет вириальных коэффициентов
Вторые
и третьи вириальные коэффициенты B(T) и C(T) природного
газа теперь определены из молярных долей ![]() и
и ![]() (входные переменные) и xCH,
(входные переменные) и xCH, ![]() и xCO (промежуточные
данные) и молярной теплоты сгорания HCH (см. рисунки В.1 и В.3)
и xCO (промежуточные
данные) и молярной теплоты сгорания HCH (см. рисунки В.1 и В.3)
В.3.1 Расчет В(Т)
Второй вириальный коэффициент B(T) рассчитывают из уравнения (В.12) с помощью процедуры, описанной в В.2.2 для температуры
T = t + 273,15. (В.27)
Рисунок В.3 - Блок-схема вычисления фактора сжимаемости
В.3.2 Расчет C(T)
Третий вириальный коэффициент C природного газа при температуре определяют из следующего уравнения
Отсутствие в уравнении (В.28) ряда членов не снижает точности расчета, поэтому они исключены из уравнения.
Кроме того, в уравнении (В.28):
где сH0, сН1 и сН2 - полиномы второй степени по отношению к температуре, т.е.:
 (B.30)
(B.30)
при этом C222, C333. C444, C115, C223 и C233 могут быть представлены в виде:
![]() (B.31)
(B.31)
Значения коэффициентов в уравнениях (В.30) и (В.31) приведены в таблице В.3.
Таблица В.3 - Числовые значения коэффициентов c(0), c(1) и c(2) в температурном разложении третьего вириального коэффициента для чистых газов и перекрестных вириальных коэффициентов (единица величины c - м6 · кмоль-2, если температура задана в кельвинах)
|
ijk |
c(0) |
c(1) |
c(2) |
|
|
СН |
Н0 |
-302488 · 10-1 |
195861 · 10-3 |
-316302 · 10-6 |
|
СН |
Н1 |
646422 · 10-4 |
-422876 · 10-6 |
688157 · 10-9 |
|
СН |
Н0 |
-302488 · 10-1 |
195861 · 10-3 |
-316302 · 10-6 |
|
СН |
Н1 |
646422 · 10-4 |
-422876 · 10-6 |
688157 · 10-9 |
|
СН |
Н2 |
-332805 · 10-7 |
223160 · 10-9 |
-367713 · 10-12 |
|
N2 |
222 |
784980 · 10-3 |
-398950 · 10-5 |
611870 · 10-8 |
|
СО2 |
333 |
205130 · 10-3 |
348880 · 10-5 |
-837030 · 10-8 |
|
Н2 |
444 |
104711 · 10-3 |
-364887 · 10-6 |
467095 · 10-9 |
|
СН + СН + N2 |
112 |
y = 0,92 + 0,0013(T - 270) |
||
|
СН + СН + СO2 |
113 |
y = 0,92 |
||
|
СН + СН + Н2 |
114 |
y = 1,20 |
||
|
СН + СН + СО |
115 |
736748 · 10-3 |
-276578 · 10-5 |
343051 · 10-8 |
|
СН + N2 + N2 |
122 |
y = 0,92 + 0,0013(T - 270) |
||
|
СН + N2 + СO2 |
123 |
y = 1,10 |
||
|
СН + СO2 + СO2 |
133 |
y = 0,92 |
||
|
N2 + N2 + СO2 |
223 |
552066 · 10-3 |
-168609 · 10-5 |
157169 · 10-8 |
|
N2 + СO2 + СO2 |
233 |
358783 · 10-3 |
806674 · 10-6 |
-325798 · 10-8 |
Другие перекрестные вириальные коэффициенты вычисляют с помощью уравнения
где yijk определяют в виде:
y112 = y122 = 0,92 + 0,0013(T - 270); (В.33)
y113 = y133 = 0,92; (B.34)
y114 = 1,20; (В.35)
y123 = 1,10. (В.36)
Уравнение (В.32) показывает, что температурная зависимость перекрестных вириальных коэффициентов по существу определяется температурной зависимостью третьих вириальных коэффициентов для чистых компонентов.
В.4 Расчет фактора сжимаемости и молярной плотности
Самый последний этап в вычислении фактора сжимаемости и молярной плотности заключается в совместном решении уравнений (1) и (2) для данного значения давления p. В качестве первого приближения в итерациях, используя w, представляют ρm в виде
![]() (В.37)
(В.37)
где второй вириальный коэффициент B определяют по уравнению (В.12) для температуры T (см. рисунок В.3). Расчетное значение ρm(w) тогда определяют по формуле
где третий смесевой вириальный коэффициент C для данной температуры T определяют из уравнения (В.28). Критерий сходимости для итераций с использованием w состоит в том, что абсолютная разность между расчетным давлением p(w), полученным из уравнения (В.39), и заданным давлением p должна быть менее чем 10-5 [см. уравнение (В.40)].
|p - p(w)| < 10-5. (В.40)
Если это условие не выполнено, то текущее значение молярной плотности ρm(w) используют в качестве нового значения ρm(w - 1) в уравнении (В.38) и рассчитывают следующее значение молярной плотности ρm(w).
Однако если левая часть уравнения (В.40) становится меньше, чем 10-5, итерации заканчивают и ρm(w) считают конечным значением молярной плотности ρm. Фактор сжимаемости тогда вычисляют по уравнению
![]() (B.41)
(B.41)
Примечание - Массовая плотность может быть вычислена следующим образом:
Перед тем как использовать Z и Zn в расчетах плотности, их значения округляют до четырех значащих цифр после запятой.
Результаты вычисления плотности представляют с тремя значащими цифрами.
В.5 Проверки на согласованность при использовании метода SGERG-88
При вычислениях методом SGERG должны быть применены следующие тесты, которые обеспечивают частичные проверки на согласованность исходных данных:
a) исходные данные должны удовлетворять следующему условию
![]() (В.43)
(В.43)
b) промежуточные расчетные значения молярных концентраций азота должны удовлетворять следующим условиям:
![]() (В.44)
(В.44)
![]() (В.45)
(В.45)
c) кроме того, внутренняя согласованность исходных данных для третьего итеративного цикла должна удовлетворять условию
Приложение С
(обязательное)
В качестве контрольных примеров для проверки компьютерной реализации метода SGERG-88 необходимо использовать следующие результаты, не приведенные в приложении В. Вычисления выполнены с использованием утвержденной программы GERG-88.ЕХЕ, которая включает в себя подпрограмму SGERG.FOR, описанную в приложении В.
Таблица С.1 - Исходные данные
|
Входная переменная |
Газ 1 |
Газ 2 |
Газ 3 |
Газ 4 |
Газ 5 |
Газ 6 |
|
|
0,006 |
0,005 |
0,015 |
0,016 |
0,076 |
0,011 |
|
|
0,000 |
0,000 |
0,000 |
0,095 |
0,000 |
0,000 |
|
D |
0,581 |
0,609 |
0,650 |
0,599 |
0,686 |
0,644 |
|
HS (МДж · м-3) |
40,66 |
40,62 |
43,53 |
34,16 |
36,64 |
36,58 |
Таблица С.2 - Результаты (значения Z)
|
Условия |
Газ 1 |
Газ 2 |
Газ 3 |
Газ 4 |
Газ 5 |
Газ 6 |
|
|
P, бар |
t, °C |
||||||
|
60 |
-3,15 |
0,84084 |
0,83397 |
0,79415 |
0,88569 |
0,82664 |
0,85406 |
|
60 |
6,85 |
0,86202 |
0,85615 |
0,82210 |
0,90150 |
0,85017 |
0,87388 |
|
60 |
16,85 |
0,88007 |
0,87500 |
0,84553 |
0,91507 |
0,87003 |
0,89071 |
|
60 |
36,85 |
0,90881 |
0,90491 |
0,88223 |
0,93684 |
0,90124 |
0,91736 |
|
60 |
56,85 |
0,92996 |
0,92690 |
0,90893 |
0,95302 |
0,92394 |
0,93690 |
|
120 |
-3,15 |
0,72146 |
0,71140 |
0,64322 |
0,80843 |
0,69557 |
0,74939 |
|
120 |
6,85 |
0,75969 |
0,75079 |
0,69062 |
0,83613 |
0,73828 |
0,78473 |
|
120 |
16,85 |
0,79257 |
0,78472 |
0,73196 |
0,85999 |
0,77463 |
0,81490 |
|
120 |
36,85 |
0,84492 |
0,83877 |
0,79778 |
0,89827 |
0,83166 |
0,86266 |
|
120 |
56,85 |
0,88322 |
0,87832 |
0,84554 |
0,92662 |
0,87269 |
0,89749 |
Представленные газы 1 - 6 - те же самые шесть газов, которые были рассмотрены в ГОСТ Р 8.662 (приложение С), где приведены полные молярные компонентные составы.
Приложение D
(обязательное)
D.1 Стандартные условия
Стандартные условия, для которых разработано стандартное вириальное уравнение GERG-88 и которые используют в подпрограмме SGERG.FOR, следующие:
- условия измерения теплоты сгорания T1 = 298,15 К (t1 = 25 °C);
Р = 101325 кПа;
- условия измерения количества газа T2 = 273,15 К (t2 = 0 oC);
Р = 101325 кПа.
Последний перечень условий представляет собой стандартные условия для относительной плотности.
Необходимо обеспечить корректное использование стандартных входных значений для теплоты сгорания и относительной плотности. Ряд стран, как правило, используют вышеприведенные условия, но иные страны используют альтернативные условия. Это может легко приводить к разночтениям, особенно до тех пор, пока в качестве единицы измерения теплоты сгорания в каждом случае может быть использован МДж · м-3. В таблице D.1 приведены стандартные условия, принятые в странах, относящихся к основным в области торговли газом.
Для тех стран, которые используют неметрические единицы для теплоты сгорания (т.е. Бет · фут-3), необходимо вводить преобразования как единиц величин, так и стандартных условий.
Используемые коэффициенты преобразования взяты из банка данных GERG.
Таблица D.1 - Принятые в странах метрические стандартные условия для измерения теплоты сгорания
|
t1 (°C) |
t2 (°C) |
|
|
Австралия |
15 |
15 |
|
Австрия |
25 |
0 |
|
Бельгия |
25 |
0 |
|
Канада |
15 |
15 |
|
Дания |
25 |
0 |
|
Франция |
0 |
0 |
|
Германия |
25 |
0 |
|
Ирландия |
15 |
15 |
|
Италия |
25 |
0 |
|
Япония |
0 |
0 |
|
Нидерланды |
25 |
0 |
|
Российская Федерация |
25 |
0 или 20 |
|
Соединенное Королевство |
15 |
15 |
|
Соединенные Штаты Америки |
15 |
15 |
|
Примечания 1 Во всех странах стандартное давление - 101325 кПа (= 101325 бар). 2 t1 - стандартная температура сгорания. 3 t2 - стандартная температура измерений. |
||
D.2 Единицы и коэффициенты преобразования для давления и температуры
Если входные переменные p и t заданы не в установленных единицах (бар и °C), то необходимо выполнить преобразования, чтобы использовать ФОРТРАН-программу. Набор соответствующих коэффициентов преобразования приведен в таблице D.2.
Таблица D.2 - Коэффициенты преобразования для давления и температуры
|
p (бар) = [p (кПа)]/100 |
|
p (бар) = [p (МПа)] · 10 |
|
p (бар) = [p (атм)] · 1,01325 |
|
p (бар) = [p (фунт/кв. дюйм (абс.))]/14,5038 |
|
p (бар) = [p (фунт/кв. дюйм (изб.)) + 14,6959]/14,5038 |
|
Температура |
|
t (°C) = T (К) - 273,15 |
|
t (°C) = [t (°F)-32]/1,8 |
|
t (°C) = [t (°R)]/1,8 - 273,15 |
D.3 Единицы величин и коэффициенты преобразования между справочными условиями для теплоты сгорания и плотности
Поскольку как высшая теплота сгорания, так и относительная плотность - функции состава газовой смеси, а теплофизические свойства отдельных компонентов газа, в свою очередь, зависят от температуры и давления, в принципе невозможно (без знания состава) преобразовать значения теплоты сгорания и относительной плотности, известные при одном перечне стандартных условий, в точно соответствующие значения для любого другого перечня стандартных условий.
Однако из-за того, что соответствующие стандартные условия всегда термодинамически близки друг к другу, а природные газы радикально не изменяются по составу, существует возможность при пересчете физических свойств практически задать такие коэффициенты преобразования, которые могут быть применены к любому типичному природному газу без снижения точности.
D.3.1 Коэффициенты преобразования для единиц величин
Если входная переменная HS задана не в установленных единицах МДж · м-3, то необходимо выполнить преобразование. Соответствующие коэффициенты преобразования для теплоты сгорания в установленном перечне стандартных условий (см. D.1) приведены в таблице D.3.
Таблица D.3 - Коэффициенты преобразования для теплоты сгорания
|
HS (МДж · м-3) = [HS (кВт-ч · м-3)]3,6 |
|
HS (МДж · м-3) = [HS (Бет · фут-3)]/26,8392 |
D.3.2 Преобразование между различными стандартными условиями
Если входные переменные HS и d заданы не при установленных стандартных условиях (см. D.1), то необходимо выполнить преобразование. В таблице D.4 приведены коэффициенты преобразования, соответствующие стандартным условиям в таблице D.1.
Таблица D.4 - Коэффициенты преобразования для теплоты сгорания и относительной плотности
|
Теплота сгорания HS при стандартных условиях t1 = 25 °C, t2 = 0 °C, p2 = 1,01325 бар: HS = HS (= 0 °C, t2 = 0 °C, p2 = 1,01325 бар) · 0,9974 HS = HS (= 15 °C, t2 = 15 °C, p2 = 1,01325 бар) · 1,0543 HS = HS (= 60 °F, t2 = 60 °F, p2 = 1,01592 бар) · 1,0535 HS = HS (= 60 °F, t2 = 60 °F, p2 = 1,01560 бар) · 1,0539 Относительная плотность d при стандартных условиях t2 = 0 °C, p2 = 1,01325 бар: d = d(t2 = 15 °C, p2 = 1,01325 бар) · 1,0002 d = d(t2 = 60 °F, p2 = 1,01592 бар или 1,01560 бар) · 1,0002 |
|
Примечание - р = 1,01560 бар = 14,73 фунт/(кв. дюйм (абс.)) (единицы давления, принятые в США). |
Приложение Е
(справочное)
Возможности распространения метода на расширенные диапазоны применения
Стандартное вириальное уравнение GERG в диапазоне температуры 263 - 338 K и давлении до 12 МПа было всесторонне сверено с данными из банка данных GERG и данными Чикагского института газовых исследований в пределах диапазонов молярных долей компонентов, высшей теплоты сгорания и относительной плотности, приведенных для газов, подготовленных к транспортированию и распределению по магистральным газопроводам (см. 4.4.1). Внутри этих пределов расширенные неопределенности расчетных результатов остаются такими, как приведены в 4.5.
Грубые оценки неопределенности расчетных результатов, включенные в расчеты факторов сжимаемости для более широких областей применения, приведены на рисунках Е.1 - Е.4 в виде графиков в координатах давление - содержание азота, диоксида углерода, этана и пропана соответственно.
На графиках рисунков Е.1 - Е.4 проиллюстрирована применимость уравнения SGERG до максимального давления 30 МПа. Эта иллюстрация служит только справочным целям и не означает того, что уравнение обычно или некритично было использовано выше установленных в настоящем стандарте пределов. Пределы неопределенности расчетных результатов зависят от давления, температуры и состава, а также существенно зависят от близости границы фазовых переходов. Предполагаемые пределы неопределенности, представленные ниже, основаны на менее исчерпывающих данных, опубликованных как дополнение к банку данных GERG, и на ряде других данных.
Во всех случаях указаны максимальные пределы неопределенности. Пунктирные линии приведены с целью отделить две области предполагаемой неопределенности в том случае, когда экспериментальных данных недостаточно, чтобы установить положение границы фаз. Состав газа будет оказывать значимое влияние на положение границы фаз, и пользователь поэтому обязан самостоятельно рассчитать границу фазовых переходов.
Конечные результаты могут быть получены при давлении до 10 МПа и температуре в диапазоне 263 - 338 К. В этих диапазонах давления и температуры только у газов, имеющих молярные доли компонентов в пределах, приведенных ниже в таблице Е.1 неопределенности расчетных результатов будут находиться в пределах ±0,1 %, ±0,2 % и ±0,5 % соответственно.
Таблица Е.1 - Предполагаемые пределы неопределенности для расширенных диапазонов применения метода
|
Молярная доля компонента для неопределенности расчетных результатов в пределах |
|||
|
±0,1 % |
±0,2 % |
±0,5 % |
|
|
Азот |
< 0,20 |
< 0,50 |
- |
|
Диоксид углерода |
< 0,09 |
< 0,12 |
< 0,23 |
|
Этан |
< 0,10 |
< 0,11 |
< 0,12 |
|
Пропан |
< 0,035 |
< 0,04 |
< 0,045 |
Уравнение SGERG-88 (T = 263 - 338 К)
p - давление; ![]() - молярная доля
азота; 1 - UZ £
±
0,1 %; 2 - UZ
от ±
0,1 % до ± 0,2 %;
- молярная доля
азота; 1 - UZ £
±
0,1 %; 2 - UZ
от ±
0,1 % до ± 0,2 %;
3 - UZ
от ±
0,2 % до ± 0,5 %; 4 - UZ от ± 0,5 % до ±
3,0 %
Рисунок Е.1 -
Предполагаемый предел расширенной неопределенности при вычислении
фактора сжимаемости природных газов с высоким содержанием азота

Уравнение SGERG-88 (T = 263 - 338 К)
p - давление; ![]() - молярная доля
диоксида углерода; 1 - UZ £ ±
0,1 %; 2 - UZ
от ±
0,1 % до ± 0,2 %;
- молярная доля
диоксида углерода; 1 - UZ £ ±
0,1 %; 2 - UZ
от ±
0,1 % до ± 0,2 %;
3 - UZ
от ±
0,2 % до ± 0,5 %; 4 - UZ от ± 0,5 % до ±
3,0 %
Рисунок
Е.2 - Предполагаемый предел расширенной неопределенности при вычислении
фактора сжимаемости природных газов с высоким содержанием диоксида углерода
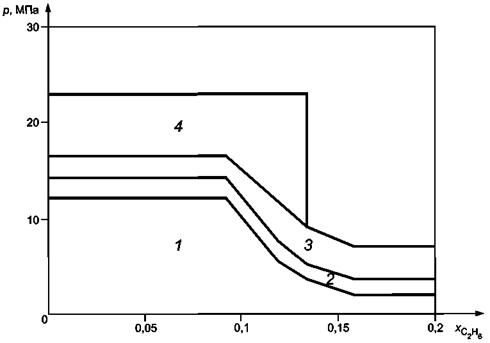
Уравнение SGERG-88 (T = 263 - 338 К)
p - давление; ![]() - молярная доля
этана; 1 - UZ £
±
0,1 %; 2 - UZ
от ±
0,1 % до ± 0,2 %;
- молярная доля
этана; 1 - UZ £
±
0,1 %; 2 - UZ
от ±
0,1 % до ± 0,2 %;
3 - UZ
от ±
0,2 % до ± 0,5 %; 4 - UZ от ±
0,5 % до ± 3,0 %
Рисунок Е.3 -
Предполагаемый предел расширенной неопределенности при вычислении
фактора сжимаемости природных газов с высоким содержанием этана
Уравнение SGERG-88 (T = 263 - 338 К)
p - давление; ![]() - молярная доля
пропана; 1 - UZ £
±
0,1 %; 2 - UZ
от ±
0,1 % до ± 0,2 %;
- молярная доля
пропана; 1 - UZ £
±
0,1 %; 2 - UZ
от ±
0,1 % до ± 0,2 %;
3 - UZ от ±
0,2 % до ± 0,5 %; 4 - UZ от ±
0,5 % до ± 3,0 %
Рисунок
Е.4 - Предполагаемый предел расширенной неопределенности при вычислении
фактора сжимаемости природных газов с высоким содержанием пропана
Приложение F
(справочное)
Подпрограмма SGERG.FOR на языке FORTRAN
Комментарий
к программе.
Вириальное уравнение состояния GERG-88.
Подпрограмма SGERG
SGERG рассчитывает фактор сжимаемости природного газа с использованием неполного компонентного состава газа.
Легальные копии этой программы могут быть получены у членов рабочей группы GERG по определению фактора сжимаемости природного газа в той версии, которая представлена в Технической монографии ТМ 5 (GERG, 1991).
Расчеты основаны на следующих исходных данных:
Допустимые интервалы:
|
- 1 - Х3: молярная доля СO2 |
от 0,0 до 0,3; |
|
- 2 - HS: теплота сгорания МДж · м-3* |
от 20 до 48; |
|
- 3 - RM: относительная плотность* |
от 0,55 до 0,9; |
|
- 4 - Х5: молярная доля Н2 |
от 0,0 до 0,1. |
_______
* Измерения количества при T = 0,0 °C; p = 1,01325 бар; температура сгорания: 25,0 °C.
Далее вводят входные переменные:
|
р - давление, бар; |
от 0 до 120; |
|
Т - температура, °C |
от -23 до +65. |
В программе рассчитывают Х2 - молярную долю азота и выводят ее на печать.
Результаты вычислений:
Z - фактор сжимаемости;
D - молярная плотность, моль · м-3.
СИНТАКСИС: CALL SGERG (X2, Х3, HS, RM, X5, Р, ТС, Z, D).
Значения коэффициентов, используемых в этой программе, соответствуют значениям, приведенным в подпрограмме GAS682 от 20 июля 1988 г., приложенной в сообщении 8807 Лаборатории Ван-дер-Ваальса, Амстердам.
J.P.J.
Michels, J.A. Schouten,
August 16, 1991
Значения газовой постоянной, молярных масс, значения теплоты сгорания и плотности воздуха соответствуют приведенным в ГОСТ 31369.
c
сссссссссссссссссссссссссссссссссссссссссссссссссссссс
c
SUBROUTINE SGERG(X2,X3,HS,RM,X5,P,TC,Z,D)
IMPLICIT DOUBLE PRECISION (A-H,O-Z)
IF(P.LT. 0.0.OR.P.GT.120.0) STOP' PRESSURE OUT OF RANGE'
IF(TC.LT.-23.0.OR. TC.GT.65.0) STOP' TEMPERATURE OUT OF RANGE'
CALL SGERG1(P,TC,X2,X3,X5,HS,RM,Z,D)
RETURN
END
C **********************************************************************
SUBROUTINE SGERG1(P,TC,Q2,Q3,Q5,QM,RM,Z,D)
IMPLICIT DOUBLE PRECISION (A-H.O-Z)
COMMON/RBLOK/AMOL,HS
COMMON/XBLOK/X1,X2,X3,X11,X12,X13,X22,X23,X33
> ,X5,X7,X15,X17,X25,X55,X77
COMMON/MBLOK/GM1R0,GM1R1,GM2,GM3,GM5,GM7,FA,FB,RL,T0,H5,H7,R
HS = QM
X3 = Q3
X5 = Q5
С IF(RM.LT. 0.55.OR. RM.GT. 0.90) STOP 'REL. MASS OUT OF RANGE'
С IF(X3.LT. 0.0.OR. X3.GT. 0.30) STOP 'CO2 OUT OF RANGE'
С IF(HS.LT.20.0.OR. HS.GT.48.0) STOP 'CALOR. VALUE OUT OF RANGE'
IF((0.55+0.97*X3-0.45*X5).GT.RM) TOP 'CONFLICTING INPUT'
SM = RM*RL
X7 = X5*0.0964D0
X33 = X3*X3
X55 = X5*X5
X77 = X7*X7
BEFF = -0.065D0
H = 1000.0D0
AMOL = 1.0D0/(FA+BEFF)
K = 0
KK = 0
1 CALL SMBER(H,SMT1)
IF(ABS(SM-SMT1).GT. 1.D-6) THEN
CALL SMBER(H+1.0D0,SMT2)
DH = (SM-SMT1)/(SMT2-SMT1)
H = H+DH
KK = KK+1
IF(KK.GT.20) STOP 'NO CONVERGENCY#1'
GO TO 1
END IF
X11 = X1*X1
X12 = X1*X2
X13 = X1*X3
X22 = X2*X2
X23 = X2*X3
X25 = X2*X5
X15 = X1*X5
X17 = X1*X7
CALL B11BER(T0,H,B11)
CALL BBER(T0,B11,BEFF)
AMOL = 1.0D0/(FA+BEFF)
HSBER = X1*H*AMOL+(X5*H5+X7*H7)*AMOL
IF(ABS(HS-HSBER).GT.1.0D-4) THEN
K = K+1
IF(K.GT.20) STOP 'NO CONVERGENCY#2'
GO TO 1
END IF
IF(X2.LT.-0.01.OR. X2.GT.0.5) STOP 'CALC. N2 OUT OF RANGE'
IF(X2+X3.GT.0.5) STOP 'N2 + CO2 OUT OF RANGE'
IF(0.55+.4*X2+0.97*X3-0.45*X5).GT.RM)
+ STOP 'CONFLICTING RESULT FOR N2'
Q2 = X2
T = TC+TO
CALL B11BER(T,H,B11)
CALL BBER(T,B11,B)
CALL CBER(T,H,C)
CALL ITER(P,T,B,C,V,Z)
D = 1.0D0/V
END
SUBROUTINE SMBER(H,SM)
IMPLICIT DOUBLE PRECISION (A-H,O-Z)
COMMON/RBLOK/AMOL,HS
COMMON/XBLOK/X1,X2,X3,X11,X12,X13,X22,X23,X33
> ,X5,X7,X15,X17,X25,X55,X77
COMMON/MBLOK/GM1R0,GM1R1,GM2,GM3,GM5,GM7,FA,FB,RL,T0,H5,H7,R
GM1 = GM1R0+GM1R1*H
X1 = (HS-(X5*H5+X7*H7)*AMOL)/H/AMOL
X2 = 1.0D0-X1-X3-X5-X7
SM = (X1*GM1+X2*GM2+X3*GM3+X5*GM5+X7*GM7)*AMOL
END
С
C *******************************************************************
SUBROUTINE B11BER(T,H,B11)
IMPLICIT DOUBLE PRECISION (A-H,O-Z)
COMMON/BBLOK/BR11H0(3), BR11H1(3), BR11H2(3), BR22(3), BR23(3),
+ BR33(3), BR15(3), BR17(3), BR55(3), BR77(3), B25
T2 = T*T
B11 = BR11H0(1) + BR11 H0(2)*T + BR11H0(3)*T2
+ + (BR11H1(1) + BR11H1(2)*T + BR11H1(3)*T2)*H
+ + (BR11H2(1) + BR11H2(2)*T + BR11H2(3)*T2)*H*H
END
C *************************************************************************
SUBROUTINE BBER(T,B11,BEFF)
IMPLICIT DOUBLE PRECISION (A-H,O-Z)
COMMON/BBLOK/BR11H0(3), BR11H1(3), BR11H2(3), BR22(3), BR23(3),
+ BR33(3), BR15(3), BR17(3), BR55(3), BR77(3), B25
COMMON/ZETA/Z12,Z13,Y12,Y13,Y123,Y115
COMMON/XBLOK/X1,X2,X3,X11,X12,X13,X22,X23,X33
> ,X5,X7,X15,X17,X25,X55,X77
T2 = T*T
B22 = BR22(1) + BR22(2)*T + BR22(3)*T2
B23 = BR23(1) + BR23(2)*T + BR23(3)*T2
B33 = BR33(1) + BR33(2)*T + BR33(3)*T2
B15 = BR15(1) + BR15(2)*T + BR15(3)*T2
B55 = BR55(1) + BR55(2)*T + BR55(3)*T2
B17 = BR17(1) + BR17(2)*T + BR17(3)*T2
B77 = BR77(1) + BR77(2)*T + BR77(3)*T2
BA13 = B11*B33
IF (BA13.LT.0.0) STOP 'NO SOLUTION'
ZZZ = Z12+(320.0D0-T)**2*1.875D-5
BEFF = Х11*В11+X12*ZZZ*(B11+B22)+2.0D0*X13*Z13*DSQRT(BA13)
> +X22*B22+2.0D0*X23*B23+X33*B33+X55*B55
> +2.0D0*X15*B15+2.0D0*X25*B25+2.0D0*X17*B17+X77*B77
END
C *******************************************************************
SUBROUTINE CBER(T,H,CEFF)
IMPLICIT DOUBLE PRECISION (A-H,O-Z)
COMMON/CBLOK/CR111H0(3), CR111H1 (3), CR111H2(3), CR222(3),
+ CR223(3), CR233(3), CR333(3), CR555(3), CR117(3)
COMMON/ZETA/Z12,Z13,Y12,Y13,Y123,Y115
COMMON/XBLOK/X1,X2,X3,X11,X12,X13,X22,X23,X33
> ,X5,X7,X15,X17,X25,X55,X77
T2 = T*T
C111 = CR111H0(1) + CR111H0(2)*T + CR111H0(3)*T2
+ + (CR111H1(1) + CR111H1(2)*T + CR111H1(3)*T2)*H
+ + (CR111H2(1) + CR111H2(2)*T + CR111H2(3)*T2)*H*H
C222 = CR222(1) + CR222(2)*T + CR222(3)*T2
C223 = CR223(1) + CR223(2)*T + CR223(3)*T2
C233 = CR233(1) + CR233(2)*T + CR233(3)*T2
C333 = CR333(1) + CR333(2)*T + CR333(3)*T2
C555 = CR555(1) + CR555(2)*T + CR555(3)*T2
C117 = CR117(1) + CR117(2)*T + CR117(3)*T2
CA112 = C111*C111*C222
CA113 = C111*C111*C333
CA122 = C111*C222*C222
CA123 = C111*C222*C333
CA133 = C111*C333*C333
CA115 = C111*C111*C555
IF (CA112.LT.0.0.OR. CA113.LT.0.0.OR. CA122.LT.0.0
+ .OR. CA123.LT.0.0.OR. CA133.LT.0.0.OR. CA115.LT.0.0)
D3REP = 1.0D0/3.0D0
CEFF = X1*X11*C111+3.0D0*X11*X2*(CA112)**D3REP*(Y12+(T-270.0D0)
+ *0.0013D0)
+ + 3.0D0*X11*X3 *(CA113)**D3REP *Y13
+ + 3.0D0*X1*X15 *(CA115)**D3REP *Y115
+ + 3.0D0*X1*X22 *(CA122)**D3REP *(Y12+(T-270.0D0)*0.0013D0)
+ + 6.0D0*X1*X2*X3*(CA123)**D3REP *Y123
+ + 3.0D0*X1*X33 *(CA133)**D3REP *Y13
+ + X22*X2*C222 + 3.0D0*X22*X3*C223 + 3.0D0*X2*X33*C233
+ + X3*X33*C333 + X5*X55*C555 + 3.0D0*X11*X7*C117
RETURN
END
C *********************************************************************
SUBROUTINE ITER(P,T,B,C,V,Z)
IMPLICIT DOUBLE PRECISION (A-H,O-Z)
COMMON/MBLOK/GM1R0,GM1R1,GM2,GM3,GM5,GM7,FA,FB,RL,T0,H5,H7,R
RT = R*T
RTP = RT/P
V = RTP+B
KK = 0
5 V = RTP*(1.0D0+B/V+C/V**2)
KK = KK+1
IF (KK.GT.20) STOP 'NO CONVERGENCY#3'
Z = 1.0D0+B/V+C/V**2
PA=RT/V*Z
IF (ABS(PA-P).GE. 1.D-5) GO TO 5
RETURN
END
C *************************************************************************
BLOCK DATA
IMPLICIT DOUBLE PRECISION (A-H,O-Z)
COMMON/BBLOK/BR11H0(3), BR11H1(3), BR11H2(3), BR22(3), BR23(3),
+ BR33(3), BR15(3), BR17(3), BR55(3), BR77(3), B25
COMMON/CBLOK/CR111H0(3), CR111H1(3), CR111H2(3), CR222(3),
+ CR223(3), CR233(3), CR333(3), CR555(3), CR117(3)
COMMON/ZETA/Z12,Z13,Y12,Y13,Y123,Y115
COMMON/MBLOK/GM1R0,GM1R1,GM2,GM3,GM5,GM7,FA,FB,RL,T0,H5,H7,R
DATA BR11H0/-0.425468D0, 0.286500D-2, -.462073D-5/,
+ BR11H1/0.877118D-3, -.556281D-5, 0.881510D-8/,
+ BR11H2/-.824747D-6, 0.431436D-8, -.608319D-11/,
+ BR22 / -.144600D0, 0.740910D-3, -.911950D-6/,
+ BR23 / -.339693D0, 0.161176D-2, -.204429D-5/,
+ BR33 / -.868340D0, 0.403760D-2, -.516570D-5/,
+ BR15 / -.521280D-1, 0.271570D-3,-.25 D-6/,
+ BR17 / -.687290D-1, -.239381D-5, 0.518195D-6/,
+ BR55 / -.110596D-2, 0.813385D-4,-.987220D-7/,
+ BR77 / -.130820D0, 0.602540D-3,-.644300D-6/,
+ B25 / 0.012D0/
DATA CR111H0/-.302488D0,0.195861D-2,-.316302D-5/,
+ CR111H1/0.646422D-3,-.422876D-5, 0.688157D-8/,
+ CR111H2/-.332805D-6, 0.223160D-8,-.367713D-11/,
+ CR222 /0.784980D-2, -.398950D-4, 0.611870D-7/,
+ CR223 /0.552066D-2, -.168609D-4, 0.157169D-7/,
+ CR233 /0.358783D-2, 0.806674D-5,-.325798D-7/,
+ CR333 /0.205130D-2, 0.348880D-4, -.837030D-7/,
+ CR555 /0.104711D-2, -.364887D-5, -.467095D-8/,
+ CR117 /0.736748D-2, -.276578D-4, -.343051D-7/
DATA Z12 /0.72D0/, Z13/-.865D0/,
+ Y12 /0.92D0/, Y13/0.92D0/, Y123/1.10D0/,
+ Y115/1.2D0/
DATA GM1R0/-2.709328D0/, GM1R1/.021062199D0/,
+ GM2 / 28.0135D0/, GM3 / 44.010D0/,
+ GM5 / 2.0159D0/, GM7 / 28.010D0/,
+ FA /22.414097D0/, FB / 22.710811 DO/,
+ RL / 1.292923D0/, T0 / 273.15D0/,
+ H5 / 285.83D0/, H7 / 282.98D0/
+ R /0.0831451 D0/
END
С
С
Приложение ДА
(справочное)
Таблица ДА.1
|
Структура настоящего стандарта |
Структура международного стандарта ИСО 12213-3:2006 |
|
1 Область применения (1) |
1 Область применения |
|
2 Нормативные ссылки (2) |
2 Нормативные ссылки |
|
3 Термины, определения и обозначения (-) |
3 Термины и определения |
|
3.1 Термины и определения (3) |
- |
|
3.2 Обозначения (приложение А) |
- |
|
4 Метод расчетного определения (4) |
4 Метод расчетного определения |
|
4.1 Сущность метода (4.1) |
4.1 Сущность метода |
|
4.2 Уравнение состояния SGERG-88 (4.2) |
4.2 Уравнение состояния SGERG-88 |
|
4.3 Входные переменные (4.3) |
4.3 Входные переменные |
|
4.4 Условия применения метода (4.4) |
4.4 Условия применения метода |
|
4.5 Оценка неопределенности вычислений (4.5) |
4.5 Оценка неопределенности вычислений |
|
5 Программное обеспечение метода (5) |
5 Программное обеспечение метода |
|
Приложение А Газ, подготовленный для транспортирования и распределения по магистральным газопроводам (приложение Е) |
Приложение А Условные обозначения и единицы величин |
|
Приложение В Описание метода расчета на основе уравнения состояния SGERG-88 (приложение В) |
Приложение В Описание метода расчета на основе уравнения состояния SGERG-88 |
|
Приложение С Контрольные примеры расчетов (приложение С) |
Приложение С Контрольные примеры расчетов |
|
Приложение D Коэффициенты преобразования (приложение D) |
Приложение D Коэффициенты преобразования |
|
Приложение Е Возможности распространения метода на расширенные диапазоны применения (приложение F) |
Приложение Е Газ, подготовленный для транспортирования и распределения по магистральным газопроводам |
|
Приложение F Подпрограмма SGERG.FOR на языке FORTRAN (приложение G) |
Приложение F Возможности распространения метода на расширенные диапазоны применения |
|
- |
Приложение G Подпрограмма SGERG.FOR на языке FORTRAN |
|
Приложение ДА Сопоставление структуры настоящего стандарта со структурой примененного в нем международного стандарта |
- |
|
Библиография |
Библиография |
|
Примечание - После заголовков разделов (подразделов) настоящего стандарта в скобках приведены номера аналогичных разделов (подразделов) международного стандарта. |
|
Библиография
|
[1] |
Международный стандарт ИСО 12213-1:2006 |
Природный газ. Расчетное определение фактора сжимаемости. Часть 1. Исходные положения и рекомендации |
|
(ISO 12213-1:2006) |
(Natural gas - Calculation of compression factor - Part 1: Introduction and guideilines) |
|
Ключевые слова: природный газ, термодинамические свойства, метод расчета |






 (В.12)
(В.12) (В.21)
(В.21)
 (В.28)
(В.28)
