РОССИЙСКОЕ АКЦИОНЕРНОЕ ОБЩЕСТВО ЭНЕРГЕТИКИ И ЭЛЕКТРИФИКАЦИИ «ЕЭС РОССИИ»
ДЕПАРТАМЕНТ НАУКИ И ТЕХНИКИ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ.
ИНФОРМАЦИОННО-ИЗМЕРИТЕЛЬНЫЕ СИСТЕМЫ.
МЕТОДИКА ОБРАБОТКИ
ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ
МЕТРОЛОГИЧЕСКОЙ АТТЕСТАЦИИ
РД 34.11.206-94
СЛУЖБА ПЕРЕДОВОГО ОПЫТА ОРГРЭС
Москва 1995
РАЗРАБОТАНО Акционерным обществом «Фирма по наладке, совершенствованию технологии и эксплуатации электростанций и сетей ОРГРЭС»
ИСПОЛНИТЕЛИ А.Г. АЖИКИН, С.А. СПОРЫХИН
УТВЕРЖДЕНО Департаментом науки и техники РАО «ЕЭС России» 14.01.94
Первый заместитель начальника А.П. БЕРСЕНЕВ
|
ИНФОРМАЦИОННО-ИЗМЕРИТЕЛЬНЫЕ СИСТЕМЫ. МЕТОДИКА ОБРАБОТКИ ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ МЕТРОЛОГИЧЕСКОЙ АТТЕСТАЦИИ |
РД 34.11.206-94 |
Срок действия установлен
с 01.01.95 г.
до 01.01.99 г.
Настоящие Методические указания (МУ) определяют основные положения и устанавливают методы обработки результатов многократных наблюдений, полученных при проведении метрологической аттестации (МА) в соответствии с «РД 34.11.202-87. Методические указания. Информационно-измерительные системы. Метрологическая аттестация. Организация и порядок проведения» (М.: СПО Союзтехэнерго, 1988) измерительных каналов (ИК) информационно-измерительных систем (ИИС), эксплуатируемых на предприятиях электроэнергетической отрасли.
Методические указания предназначены для персонала организаций, проводящих МА ИИС.
В МУ изложены алгоритмы обработки результатов многократных наблюдений при экспериментальных исследованиях метрологических характеристик (MX) ИК ИИС (в условиях эксплуатации) комплектным и поэлементным методами.
Указанные в МУ алгоритмы обработки экспериментальных данных основаны на следующих допущениях:
закон распределения случайной составляющей погрешности ИК является нормальным;
закон распределения случайной составляющей погрешности ИК, обусловленной гистерезисом, является равномерным;
закон распределения систематической составляющей погрешности на множестве однотипных ИК является нормальным;
взаимное влияние ИК не имеет места.
С выходом настоящих МУ утрачивают силу «Методические указания. Информационно-измерительные системы. Методика обработки экспериментальных данных метрологической аттестации: РД 34.11.206-88» (М.: СПО Союзтехэнерго, 1988).
1. ОБЩИЕ ПОЛОЖЕНИЯ
1.1. Результаты многократных наблюдений, полученные при экспериментальных исследованиях MX ИК, должны быть представлены в протоколе по форме, приведенной в РД 34.11.202-87.
Примечание. Под многократными наблюдениями следует понимать те случаи, когда осуществляется не менее четырех наблюдений.
1.2. Результатами обработки экспериментальных данных являются следующие MX:
систематическая составляющая погрешности ИК Δs или (и) математическое ожидание систематической составляющей погрешности совокупности однотипных ИК М(Δs);
среднее квадратическое отклонение (СКО) систематической составляющей погрешности ИК совокупности однотипных ИК σ(Δs);
среднее квадратическое отклонение случайной составляющей погрешности ИК σ(![]() ) или (и) совокупности однотипных ИК σ(
) или (и) совокупности однотипных ИК σ(![]() );
);
случайная составляющая погрешности ИК или (и) совокупности
однотипных ИК, обусловленная гистерезисом - вариация Н или (и) ![]() ;
;
верхняя и нижняя границы доверительного интервала погрешности измерений ИК или совокупности однотипных ИК Δh, Δl.
1.3. Результаты МА должны быть представлены в соответствии с МИ 1317-86 в виде Δh, Δl, Р (Р - доверительная вероятность).
Метрологические характеристики нормируются для групп однотипных ИК или для каждого ИК.
2. АЛГОРИТМ ОБРАБОТКИ РЕЗУЛЬТАТОВ НАБЛЮДЕНИЙ ПРИ КОМПЛЕКТНОМ МЕТОДЕ ИССЛЕДОВАНИЙ MX ИК
2.1. Обработка результатов проводится в три этапа.
На первом этапе полученная совокупность результатов наблюдений для каждого l-го ИК, в каждой j-й точке диапазона измерений проверяется на наличие грубых ошибок (погрешностей). Отдельно проверяются результаты, полученные при прямом и обратном ходах в процессе проведения эксперимента.
2.1.1. Анализируются условия, в которых был получен результат наблюдения, по предположению, содержащий грубую погрешность, т.е. резко отличающийся от остальных результатов наблюдений.
Если результат получен в тех же условиях, что и вся совокупность, и не является следствием грубых ошибок при наблюдениях, то оцениваемый результат не исключается из рассматриваемой совокупности.
Если же результат наблюдений является следствием грубых ошибок при наблюдениях или следствием случайного нарушения нормальных условий (т.е. условий, в которых получена вся совокупность), то указанный результат наблюдений не принадлежит той же совокупности, что и остальные, и исключается из дальнейшей обработки.
Если причина резкого отклонения результата наблюдений не установлена, то следует воспользоваться методом статистической обработки (п. 2.1.2).
2.1.2. Оценивается анормальность результатов наблюдений.
2.1.2.1. Определяется среднее арифметическое значение результатов наблюдений по формуле
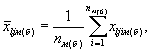 (1)
(1)
где xljiм(б) - i-e значение результата наблюдений в j-й точке диапазона измерений l-го ИК при прямом (обратном) ходе (i = 1 ... n);
nм(б) - количество наблюдений при прямом (обратном) ходе.
2.1.2.2. Определяется среднее квадратическое отклонение результатов наблюдений по формуле
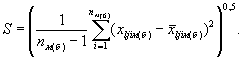 (2)
(2)
2.1.2.3. Определяется отношение U по формуле
![]() (3)
(3)
где x*ljiм(б) - результат наблюдения, по предположению, содержащий грубую погрешность.
2.1.2.4. Полученное значение U сравнивается со значением h по таблице приложения 1.
2.1.2.5. Если U > h, то результат наблюдений исключается из рассматриваемой совокупности, в этом случае проводится еще одно наблюдение. При невозможности получения дополнительного результата наблюдений исключенный результат заменяется на среднее арифметическое из двух смежных значений из протокола наблюдений.
2.1.2.6. При малом числе наблюдений для проверки совокупности результатов наблюдений на наличие грубых ошибок возможно применение критерия Диксона, который определяется следующим образом.
Определяется среднее арифметическое значение по формуле (1). Определяется модуль отклонения каждого результата наблюдений от среднего значения
Полученные значения отклонений записываются в возрастающий ряд
Δxlj1м(б) £ ... £ Δxljiм(б) £ ... £ Δxljnм(б). (5)
Определяется отношение К по формуле
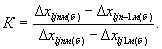 (6)
(6)
Полученное значение К сравнивается со значениями Кд из таблицы.
|
Количество результатов наблюдений nм (nб) |
||||||||||||
|
4 |
5 |
6 |
7 |
8 |
9 |
10 |
12 |
14 |
16 |
18 |
20 |
|
|
0,95 |
0,76 |
0,64 |
0,56 |
0,51 |
0,47 |
0,44 |
0,41 |
0,38 |
0,35 |
0,33 |
0,31 |
0,30 |
|
0,9 |
0,68 |
0,56 |
0,48 |
0,43 |
0,40 |
0,37 |
0,35 |
0,32 |
0,29 |
0,28 |
0,26 |
0,26 |
Если К > Кд, то результат наблюдений, у которого модуль отклонения от среднего значения является наибольшим, исключается из рассматриваемой совокупности и производится его замена, как указано в п. 2.1.2.5.
2.2. На втором этапе определяются следующие характеристики погрешности ИК.
2.2.1. Оценка систематической составляющей погрешности в j-й точке диапазона измерений l-го ИК по формуле
![]() (7)
(7)
где ![]() - среднее арифметическое значение результатов наблюдений в j-й точке диапазона измерений l-го ИК при прямом (обратном) ходе;
- среднее арифметическое значение результатов наблюдений в j-й точке диапазона измерений l-го ИК при прямом (обратном) ходе;
xдj - действительное значение измеряем ой величины в j-й точке диапазона измерений l-го ИК (действительное значение образцового сигнала на входе ИК в единицах измеряемой величины).
Значения ![]() определяются по формулам:
определяются по формулам:
 (8)
(8)
 (9)
(9)
2.2.2. Оценка дисперсии случайной составляющей погрешности в j-й точке диапазона измерений l-го ИК по формуле
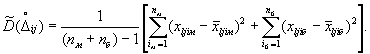 (10)
(10)
2.2.3. Оценка СКО случайной составляющей погрешности в i-й точке диапазона измерений l-го ИК по формуле
![]() (11)
(11)
2.2.4. Оценка вариаций в j-й точке диапазона измерений l-го ИК по формуле
![]() (12)
(12)
2.2.5. Если обрабатываются результаты наблюдений при исследовании совокупности однотипных ИК, то обработка продолжается и определяются следующие обобщенные характеристики погрешности совокупности ИК.
2.2.5.1. Оценка математического ожидания систематической составляющей погрешности в j-й точке диапазона измерений совокупности однотипных ИК по формуле
![]() (13)
(13)
где m - количество однотипных ИК в обрабатываемой (рассматриваемой) совокупности.
2.2.5.2. Оценка СКО систематической составляющей погрешности в j-й точке диапазона измерений совокупности однотипных ИК по формуле
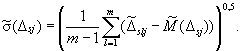 (14)
(14)
2.2.5.3. Оценка СКО случайной составляющей погрешности в j-й точке диапазона измерений, если оценки дисперсий случайной составляющей погрешности совокупности однотипных ИК однородны, по формуле
 (15)
(15)
Если же дисперсии не однородны, то в качестве ![]() принимается максимальное из т
значений
принимается максимальное из т
значений ![]() , т.е.
, т.е.
![]() (16)
(16)
Алгоритм проверки однородности дисперсий представлен в приложении 2.
2.2.5.4. Оценка вариации в j-й точке диапазона измерений совокупности однотипных ИК в случае допустимости ее расхождения по формуле
![]() (17)
(17)
Если же расхождения значений вариации не допустимо, то в качестве ![]() принимается максимальное из
их значений
принимается максимальное из
их значений ![]() , т.е.
, т.е.
![]() (18)
(18)
Алгоритм проверки допустимости расхождения вариации представлен в приложении 3.
2.3. На третьем этапе обработки в каждой j-й точке диапазона измерений ИК (совокупности однотипных ИК) определяются верхняя (Δhl) и нижняя (Δlj) границы доверительного интервала погрешности измерений.
2.3.1. Для одного ИК Δhl, Δlj определяются по формуле
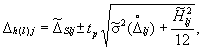 (19)
(19)
где tр - коэффициент Стьюдента, который определяется по таблице приложения 4 в зависимости от доверительной вероятности и количества наблюдений.
2.3.2. Для совокупности однотипных ИК Δhl, Δlj определяются по формуле
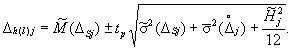 (20)
(20)
2.4. Полученные значения Δhl и Δlj записываются как функции Δhl = f(xдj) и Δlj = f(xдj), аппроксимируются по диапазону измерений прямыми (например, методом наименьших квадратов) и представляются в виде:
Δh = a1 + b1xизм; (21)
Δl = a2 + b2xизм, (22)
где a1(a2), b1(b2) - параметры аппроксимирующих прямых;
хизм - измеренное значение физической величины.
Параметры аппроксимирующих прямых для метода наименьших квадратов находятся из решения следующей системы уравнений:
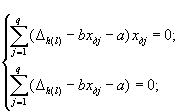 (23)
(23)
где q - количество точек диапазона измерений, в которых проводились экспериментальные исследования (j = 1 ... q).
2.5. В качестве нормированных MX ИК (совокупности ИК) во всем диапазоне измерений принимаются приведенные γh, γl и относительные δh, δl значения верхней и нижней границ доверительного интервала погрешности измерений, которые определяются по формулам:
![]() ; (24)
; (24)
![]() ; (25)
; (25)
где хв, хн - верхний и нижний пределы диапазона измерений.
Абсолютные значения границ доверительного интервала погрешности измерений ИК при измерении физической величины определяются по формулам:
![]() (28)
(28)
![]() (29)
(29)
3. АЛГОРИТМ ОБРАБОТКИ РЕЗУЛЬТАТОВ НАБЛЮДЕНИЙ ПРИ ПОЭЛЕМЕНТНОМ МЕТОДЕ ИССЛЕДОВАНИЯ МХ ИК
3.1. При поэлементном методе исследуются МХ элементов ИК. Обработка результатов наблюдений при исследовании MX элемента ИК проводится согласно пп. 2.1 - 2.3.
3.2. Границы доверительного интервала погрешности измерений определяются следующим образом.
Для одного ИК по формуле
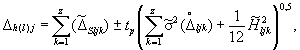 (30)
(30)
где ![]() - оценка систематической
составляющей погрешности в j-й точке диапазона измерений k-го
элемента l-го ИК;
- оценка систематической
составляющей погрешности в j-й точке диапазона измерений k-го
элемента l-го ИК;
![]() - оценка СКО случайной составляющей погрешности в j-й точке
диапазона измерений k-го элемента l-го ИК;
- оценка СКО случайной составляющей погрешности в j-й точке
диапазона измерений k-го элемента l-го ИК;
![]() - оценка
вариации в j-й точке диапазона измерений k-го
элемента l-го ИК;
- оценка
вариации в j-й точке диапазона измерений k-го
элемента l-го ИК;
z - количество элементов ИК.
Для совокупности однотипных ИК по формуле
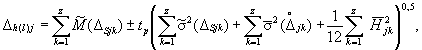 (31)
(31)
где ![]() - оценка математического ожидания систематической составляющей
погрешности в j-й точке диапазона измерений k-го
элемента совокупности однотипных ИК;
- оценка математического ожидания систематической составляющей
погрешности в j-й точке диапазона измерений k-го
элемента совокупности однотипных ИК;
![]() - оценка СКО систематической составляющей погрешности в j-й точке
диапазона измерений k-го элемента совокупности однотипных
ИК;
- оценка СКО систематической составляющей погрешности в j-й точке
диапазона измерений k-го элемента совокупности однотипных
ИК;
![]() - оценка СКО случайной составляющей погрешности в j-й точке
диапазона измерений k-го элемента совокупности однотипных
ИК;
- оценка СКО случайной составляющей погрешности в j-й точке
диапазона измерений k-го элемента совокупности однотипных
ИК;
![]() - оценка вариации в j-й
точке диапазона измерений k-го элемента совокупности
однотипных ИК.
- оценка вариации в j-й
точке диапазона измерений k-го элемента совокупности
однотипных ИК.
3.3. Если поэлементный метод исследования MX ИК является расчетно-экспериментальным, то расчет MX (составляющих погрешности в каждой j-й точке диапазона измерений) элементов ИК, не исследуемых экспериментально, следует проводить по MX агрегатных средств измерений (АСИ), входящих в состав элемента в соответствии с «Методикой определения обобщенных метрологических характеристик измерительных каналов ИИС и АСУ ТП по метрологическим характеристикам агрегатных средств измерений: МТ 34-70-038-87» (M.: СПО Союзтехэнерго, 1987).
3.4. Нормирование MX ИК (совокупности ИК) проводится согласно пп. 2.4 и 2.5.
Приложение 1
ПРЕДЕЛЬНЫЕ ЗНАЧЕНИЯ h ПРИ ОЦЕНКЕ РЕЗУЛЬТАТОВ НАБЛЮДЕНИЙ НА АНОРМАЛЬНОСТЬ
|
Предельное значение h при вероятности f |
||
|
0,90 |
0,95 |
|
|
4 |
1,42 |
1,46 |
|
5 |
1,60 |
1,67 |
|
6 |
1,73 |
1,82 |
|
7 |
1,83 |
1,94 |
|
8 |
1,91 |
2,03 |
|
9 |
1,98 |
2,11 |
|
10 |
2,03 |
2,18 |
|
11 |
2,09 |
2,23 |
|
12 |
2,13 |
2,29 |
|
13 |
2,17 |
2,33 |
|
14 |
2,21 |
2,37 |
|
15 |
2,25 |
2,41 |
|
16 |
2,28 |
2,44 |
|
17 |
2,41 |
2,48 |
|
18 |
2,34 |
2,50 |
|
19 |
2,36 |
2,53 |
|
20 |
2,38 |
2,56 |
|
25 |
2,635 |
2,870 |
|
30 |
2,696 |
2,928 |
|
40 |
2,792 |
3,015 |
|
50 |
2,860 |
3,082 |
|
100 |
3,076 |
3,285 |
|
250 |
3,339 |
3,534 |
Приложение 2
ПРОВЕРКА ОДНОРОДНОСТИ m ОЦЕНОК ДИСПЕРСИЙ
1. При m = 2 оценки дисперсий считаются однородными, если выполняется неравенство
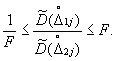
Значение F находится по табл. П2.1 в зависимости от доверительной вероятности и параметров f1 и f2, которые определяются по формуле
f1 = f2 = nм + nб - 1.
Таблица П2.1
Значения F
|
f2 |
Вероятность |
1 |
2 |
3 |
4 |
5 |
6 |
f1 7 |
8 |
9 |
10 |
11 |
12 |
15 |
20 |
24 |
30 |
40 |
100 |
∞ |
|
4 |
0,90 |
4,54 |
4,32 |
4,19 |
4,11 |
4,05 |
4,01 |
3,98 |
3,95 |
3,94 |
3,92 |
3,91 |
3,90 |
3,87 |
3,84 |
3,83 |
3,82 |
3,80 |
3,78 |
3,77 |
|
0,95 |
7,71 |
6,94 |
6,59 |
6,39 |
6,26 |
6,16 |
6,09 |
6,04 |
6,00 |
5,96 |
5,94 |
5,91 |
5,86 |
5,80 |
5,77 |
5,75 |
5,72 |
5,66 |
5,65 |
|
|
5 |
0,90 |
4,06 |
3,78 |
3,62 |
3,52 |
3,45 |
3,40 |
3,37 |
3,34 |
3,32 |
3,30 |
3,28 |
3,27 |
3,24 |
3,21 |
3,19 |
3,17 |
3,16 |
3,13 |
3,12 |
|
0,95 |
6,61 |
5,79 |
5,41 |
5,19 |
5,05 |
4,95 |
4,88 |
4,82 |
4,77 |
4,74 |
4,71 |
4,68 |
4,62 |
4,56 |
4,53 |
4,50 |
4,46 |
4,41 |
4,40 |
|
|
6 |
0,90 |
3,78 |
3,46 |
3,29 |
3,18 |
3,11 |
3,05 |
3,01 |
2,98 |
2,96 |
2,94 |
2,92 |
2,90 |
2,87 |
2,84 |
2,82 |
2,80 |
2,78 |
2,75 |
2,74 |
|
0,95 |
5,99 |
5,14 |
4,76 |
4,53 |
4,39 |
4,28 |
4,21 |
4,15 |
4,10 |
4,06 |
4,03 |
4,00 |
3,94 |
3,87 |
3,84 |
3,81 |
3,77 |
3,71 |
3,70 |
|
|
7 |
0,90 |
3,59 |
3,26 |
3,07 |
2,96 |
2,88 |
2,83 |
2,78 |
2,75 |
2,72 |
2,70 |
2,68 |
2,67 |
2,63 |
2,59 |
2,58 |
2,56 |
2,54 |
2,50 |
2,48 |
|
0,95 |
5,59 |
4,74 |
4,35 |
4,12 |
3,97 |
3,87 |
3,79 |
3,73 |
3,68 |
3,64 |
3,60 |
3,57 |
3,51 |
3,44 |
3,41 |
3,38 |
3,34 |
3,27 |
3,25 |
|
|
8 |
0,90 |
3,46 |
3,11 |
2,92 |
2,81 |
2,73 |
2,67 |
2,62 |
2,59 |
2,56 |
2,54 |
2,52 |
2,50 |
2,46 |
2,42 |
2,40 |
2,38 |
2,36 |
2,32 |
2,31 |
|
0,95 |
5,32 |
4,46 |
4,07 |
3,84 |
3,69 |
3,58 |
3,50 |
3,44 |
3,39 |
3,35 |
3,31 |
3,28 |
3,22 |
3,15 |
3,12 |
3,08 |
3,04 |
2,97 |
2,95 |
|
|
9 |
0,90 |
3,36 |
3,01 |
2,81 |
2,69 |
2,61 |
2,55 |
2,51 |
2,47 |
2,44 |
2,42 |
2,40 |
2,38 |
2,34 |
2,30 |
2,28 |
2,25 |
2,23 |
2,49 |
2,17 |
|
0,95 |
5,12 |
4,26 |
3,86 |
3,63 |
3,48 |
3,37 |
3,29 |
3,23 |
3,18 |
3,14 |
3,10 |
3,07 |
3,01 |
2,94 |
2,90 |
2,86 |
2,83 |
2,76 |
2,73 |
|
|
10 |
0,90 |
3,28 |
2,92 |
2,73 |
2,61 |
2,52 |
2,46 |
2,41 |
2,38 |
2,35 |
2,32 |
2,30 |
2,28 |
2,24 |
2,20 |
2,18 |
2,16 |
2,13 |
2,09 |
2,07 |
|
0,95 |
4,96 |
4,10 |
3,71 |
3,48 |
3,33 |
3,22 |
3,14 |
3,07 |
3,02 |
2,98 |
2,94 |
2,91 |
2,85 |
2,77 |
2,74 |
2,70 |
2,66 |
2,59 |
2,56 |
|
|
11 |
0,90 |
3,23 |
2,86 |
2,66 |
2,54 |
2,45 |
2,39 |
2,34 |
2,30 |
2,27 |
2,25 |
2,23 |
2,21 |
2,17 |
2,12 |
2,10 |
2,08 |
2,05 |
2,00 |
1,99 |
|
0,95 |
4,84 |
3,98 |
3,59 |
3,36 |
3,20 |
3,09 |
3,01 |
2,95 |
2,90 |
2,85 |
2,82 |
2,79 |
2,72 |
2,65 |
2,61 |
2,57 |
2,53 |
2,46 |
2,43 |
|
|
12 |
0,90 |
3,18 |
2,81 |
2,61 |
2,48 |
2,39 |
2,33 |
2,28 |
2,24 |
2,21 |
2,19 |
2,17 |
2,15 |
2,10 |
2,06 |
2,04 |
2,01 |
1,99 |
1,94 |
1,92 |
|
0,95 |
4,75 |
3,89 |
3,49 |
3,26 |
3,11 |
3,00 |
2,91 |
2,85 |
2,80 |
2,75 |
2,72 |
2,69 |
2,62 |
2,54 |
2,51 |
2,47 |
2,43 |
2,35 |
2,32 |
|
|
15 |
0,90 |
2,07 |
2,70 |
2,49 |
2,36 |
2,27 |
2,21 |
2,16 |
2,12 |
2,09 |
2,06 |
2,04 |
2,02 |
1,97 |
1,92 |
1,90 |
1,87 |
1,85 |
1,79 |
1,77 |
|
0,95 |
4,54 |
3,68 |
3,29 |
3,06 |
2,90 |
2,79 |
2,71 |
2,64 |
2,59 |
2,54 |
2,51 |
2,48 |
2,40 |
2,33 |
2,29 |
2,25 |
2,20 |
2,12 |
2,10 |
|
|
20 |
0,90 |
2,97 |
2,59 |
2,38 |
2,25 |
2,16 |
2,09 |
2,04 |
2,00 |
1,96 |
1,94 |
1,92 |
1,89 |
1,84 |
1,79 |
1,77 |
1,74 |
1,71 |
1,65 |
1,63 |
|
|
0,95 |
4,35 |
3,49 |
3,10 |
2,87 |
2,71 |
2,60 |
2,51 |
2,45 |
2,39 |
2,35 |
2,31 |
2,28 |
2,20 |
2,12 |
2,08 |
2,04 |
1,99 |
1,91 |
1,88 |
|
24 |
0,90 |
2,93 |
2,54 |
2,33 |
2,19 |
2,10 |
2,04 |
1,98 |
1,94 |
1,91 |
1,88 |
1,85 |
1,83 |
1,78 |
1,73 |
1,70 |
1,67 |
1,64 |
1,58 |
1,56 |
|
|
0,95 |
4,26 |
3,40 |
3,01 |
2,78 |
2,62 |
2,51 |
2,42 |
2,36 |
2,30 |
2,25 |
2,21 |
2,18 |
2,11 |
2,03 |
1,98 |
1,94 |
1,89 |
1,80 |
1,77 |
|
30 |
0,90 |
2,88 |
2,49 |
2,28 |
2,14 |
2,05 |
1,98 |
1,93 |
1,88 |
1,85 |
1,82 |
1,79 |
1,77 |
1,72 |
1,67 |
1,64 |
1,61 |
1,57 |
1,51 |
1,48 |
|
|
0,95 |
4,17 |
3,32 |
2,92 |
2,69 |
2,53 |
2,42 |
2,33 |
2,27 |
2,21 |
2,16 |
2,13 |
2,09 |
2,01 |
1,93 |
1,89 |
1,84 |
1,79 |
1,70 |
1,66 |
|
40 |
0,90 |
2,84 |
2,44 |
2,23 |
2,09 |
2,00 |
1,93 |
1,87 |
1,83 |
1,79 |
1,76 |
1,73 |
1,71 |
1,66 |
1,61 |
1,57 |
1,54 |
1,51 |
1,43 |
1,41 |
|
|
0,95 |
4,08 |
3,23 |
2,84 |
2,61 |
2,45 |
2,34 |
2,25 |
2,18 |
2,12 |
2,08 |
2,04 |
2,00 |
1,92 |
1,84 |
1,79 |
1,74 |
1,69 |
1,59 |
1,55 |
|
120 |
0,90 |
2,75 |
2,35 |
2,13 |
1,99 |
1,90 |
1,82 |
1,77 |
1,72 |
1,68 |
1,65 |
1,62 |
1,60 |
1,55 |
1,48 |
1,45 |
1,41 |
1,37 |
1,27 |
1,24 |
|
|
0,95 |
3,92 |
3,07 |
2,68 |
2,45 |
2,29 |
2,17 |
2,09 |
2,02 |
1,96 |
1,91 |
1,87 |
1,83 |
1,75 |
1,66 |
1,61 |
1,55 |
1,50 |
1,37 |
1,32 |
|
∞ |
0,90 |
2,71 |
2,30 |
2,08 |
1,94 |
1,85 |
1,77 |
1,72 |
1,67 |
1,63 |
1,60 |
1,57 |
1,55 |
1,49 |
1,42 |
1,38 |
1,34 |
1,30 |
1,18 |
1,13 |
|
|
0,95 |
3,84 |
3,00 |
2,60 |
2,47 |
2,21 |
2,10 |
2,01 |
1,94 |
1,88 |
1,83 |
1,79 |
1,75 |
1,67 |
1,57 |
1,52 |
1,46 |
1,39 |
1,24 |
1,17 |
2. При т > 2 оценки дисперсий считаются однородными, если выполняется неравенство
Gmax £ G.
Значение Gmax находится по формуле

Значения G находятся по табл. П2.2 в зависимости от числа наблюдений при доверительной вероятности 0,95.
Таблица П2.2
Значения G
|
nм + nб - 1 |
||||||||
|
7 |
8 |
9 |
10 |
16 |
36 |
144 |
∞ |
|
|
3 |
0,6530 |
0,6333 |
0,6167 |
0,6025 |
0,5466 |
0,4748 |
0,4031 |
0,3333 |
|
4 |
0,5365 |
0,5175 |
0,5017 |
0,4884 |
0,4366 |
0,3720 |
0,3093 |
0,2500 |
|
5 |
0,4564 |
0,4387 |
0,4241 |
0,4118 |
0,3645 |
0,3066 |
0,2513 |
0,2000 |
|
6 |
0,3980 |
0,3817 |
0,3682 |
0,3568 |
0,3135 |
0,2612 |
0,2119 |
0,1667 |
|
7 |
0,3535 |
0,3384 |
0,3259 |
0,3154 |
0,2756 |
0,2278 |
0,1833 |
0,1329 |
|
8 |
0,3185 |
0,3043 |
0,2926 |
0,2829 |
0,2462 |
0,2022 |
0,1616 |
0,1250 |
|
9 |
0,2901 |
0,2768 |
0,2659 |
0,2568 |
0,2226 |
0,1820 |
0,1446 |
0,1111 |
|
10 |
0,2666 |
0,2541 |
0,2439 |
0,2353 |
0,2032 |
0,1655 |
0,1308 |
0,1000 |
|
12 |
0,2299 |
0,2187 |
0,2098 |
0,2020 |
0,1737 |
0,1403 |
0,1100 |
0,0833 |
|
15 |
0,1911 |
0,1815 |
0,1736 |
0,1671 |
0,1429 |
0,1144 |
0,0889 |
0,0667 |
|
20 |
0,1501 |
0,1422 |
0,1357 |
0,1303 |
0,1108 |
0,0879 |
0,0675 |
0,0500 |
|
24 |
0,1286 |
0,1216 |
0,1160 |
0,1113 |
0,0942 |
0,0743 |
0,0567 |
0,0417 |
|
30 |
0,1061 |
0,1002 |
0,0958 |
0,0921 |
0,0771 |
0,0604 |
0,0457 |
0,0333 |
|
40 |
0,0827 |
0,0780 |
0,0745 |
0,0713 |
0,0595 |
0,0462 |
0,0347 |
0,0250 |
|
60 |
0,0583 |
0,0552 |
0,0520 |
0,0497 |
0,0411 |
0,0316 |
0,0234 |
0,0167 |
|
120 |
0,0312 |
0,0292 |
0,0279 |
0,0266 |
0,0218 |
0,0165 |
0,0120 |
0,0083 |
|
∞ |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
Приложение 3
ПРОВЕРКА ДОПУСТИМОСТИ РАСХОЖДЕНИЯ т ОЦЕНОК ВАРИАЦИИ
1. Определяется оценка межгрупповой дисперсии по формуле
![]()
2. Определяется среднее значение внутригрупповых оценок дисперсии по формуле
![]()
3. Расхождение вариации считается допустимым, если выполняется неравенство
![]()
Значение F находится по табл. П2.1 в зависимости от доверительной вероятности и параметров f1 и f2, которые определяются по формулам:
f1 = m - 1;
f2 = m(nм + nб - 1).
Приложение 4
ЗНАЧЕНИЕ КОЭФФИЦИЕНТА СТЬЮДЕНТА
|
Количество наблюдений (nм + nб - 1) |
Доверительная вероятность, Р |
|
|
0,90 |
0,95 |
|
|
4 |
2,132 |
2,776 |
|
5 |
2,015 |
2,571 |
|
6 |
1,943 |
2,447 |
|
7 |
1,895 |
2,365 |
|
8 |
1,860 |
2,306 |
|
9 |
1,833 |
2,262 |
|
10 |
1,812 |
2,228 |
|
11 |
1,796 |
2,201 |
|
12 |
1,782 |
2,179 |
|
13 |
1,771 |
2,160 |
|
14 |
1,761 |
2,145 |
|
15 |
1,753 |
2,131 |
|
16 |
1,746 |
2,120 |
|
17 |
1,740 |
2,110 |
|
18 |
1,734 |
2,101 |
|
19 |
1,729 |
2,093 |
|
20 |
1,725 |
2,086 |
|
21 |
1,721 |
2,080 |
|
22 |
1,717 |
2,074 |
|
23 |
1,714 |
2,069 |
|
24 |
1,711 |
2,064 |
|
25 |
1,708 |
2,060 |
|
26 |
1,706 |
2,056 |
|
27 |
1,703 |
2,052 |
|
28 |
1,701 |
2,048 |
|
29 |
1,699 |
2,045 |
|
30 |
1,697 |
2,042 |
|
∞ |
1,645 |
1,960 |
СОДЕРЖАНИЕ